-
目前,无论是对人工林还是天然林,大多都将乔木层视作整体研究探讨其直径分布[1-6],基于分层的直径分布研究较少[7-10]。Knoke等[8]仅对由不同林龄的人工林组成的混交林直径分布进行了描述;庄崇洋等[9]对典型中亚热带天然阔叶林各林层直径分布及变化规律的研究表明,各林层直径分布差异显著,分林层研究林分直径分布是有必要的。
半天然林是指通过造林和人工促进天然更新方式经营与调整后的森林[11],是介于人工林和天然林之间的重要的森林类型。目前国内外对半天然林的研究较少,现有报道中多以半天然杉阔混交林或半天然杉木马尾松混交林为研究对象,且研究内容多集中于林分的形成发育、树种组成和物种多样性、空间格局及群落结构等方面[12-18],在对半天然林林分直径结构的研究上,陈存及等[13]仅对半天然杉阔混交林的直径分布做简单的形状描述,尚未见从各林层和分布拟合的角度研究半天然林直径分布的报道。
本研究以半天然马尾松(Pinus massoniana Lamb.)阔叶混交林为研究对象,采用最大受光面法[19]划分林层,在对其树种组成与多样性研究的基础上[12],对半天然马尾松阔叶混交林各林层(包括全林和各亚层)的直径分布进行探讨,揭示半天然马尾松阔叶混交林全林及各林层直径分布的特点,以期为该类型林分的可持续经营提供依据。
-
研究区位于福建省永安市,地处福建中部偏西,地理位置为 116°56′~117°47′ E,25°33′~26°12′ N,总面积2 942 km2。属中亚热带海洋性季风气候,同时兼具一定的大陆性气候特点,气候温和、四季分明,年均气温14.3~19.2℃,年均降水量1 490~2 050 mm,由于地形复杂,海拔相对高差较大,导致垂直分布的小区域性气候差异更大。主要土壤类型为红壤和黄壤,地带性植被为中亚热带常绿阔叶林。
-
在永安市西洋镇岭头村58林班15大班5小班的半天然马尾松阔叶混交林中,设置 10块40 m × 20 m样地(按每个样地200株左右林木株数控制样地面积)。该林分源于1995年人工营造的马尾松纯林,造林前为混生有杉木的天然阔叶林采伐迹地,立地类型为Ⅱ类地,南坡向中坡位、坡度23°,面积为1.47 hm2,造林密度3 000株·hm−2,造林后连续3年每年2次幼林抚育,未进行过抚育间伐,停止幼林抚育后,天然更新阔叶树逐渐进入乔木层,现已形成马尾松与阔叶树混交的半天然林[12],调查时林分年龄为24 a。对样地内所有胸径 ≥ 5 cm的林木进行每木调查与定位,测定与记录种名、胸径、高度、枝下高和冠幅等因子,同时应用最大受光面法[19]确定各林木所属林层。10块样地的平均胸径范围为12.5~13.8 cm,平均高为14.3~16.2 m,株数密度为1 950~3 238株·hm−2,蓄积量为196.56~305.42 m3·hm−2。
根据最大受光面法[19],将样地内所有胸径 ≥ 5 cm的林木划分为受光层(第Ⅰ亚层,即由树冠能接收到垂直光照的林木组成的林层)和非受光层(第Ⅱ亚层,即由树冠不能接受到垂直光照的林木组成的林层),最大受光面的高度为12.6 m。删除枯死木等异常数据后,以2 cm为径阶距进行径阶整化,计算各林层的平均胸径、标准差、变异系数并统计胸径范围。10块样地全林胸径、胸径标准差和变异系数范围分别为5.0~29.5 cm、4.88~6.11和37.50%~45.13%;第Ⅰ亚层胸径、平均胸径、胸径标准差和变异系数范围分别为5.0~29.5 cm、15.0~16.9 cm、4.03~5.90和26.30%~34.88%;第Ⅱ亚层胸径、平均胸径、胸径标准差和变异系数范围分别为5.0~17.7 cm、7.6~9.2 cm、1.87~2.96和24.20%~32.19%。
-
采用Shapiro-Wilk检验(S-W检验)对各样地各林层的直径分布进行正态性检验。利用偏度和峰度指标描述直径分布的偏离程度和离散程度。参考前人对直径分布的研究成果[1-2,5,9-10,20-25],本研究选用Weibull分布、Meyer负指数函数对各样地各林层直径分布进行拟合,用χ2检验法对拟合效果进行检验。
-
偏度(SK)和峰度(KT)系数是描述数据分布形态的统计量。偏度体现数据分布的对称性或拖尾程度,偏度小于0表示为左偏(负偏态),即绝大多数值位于平均值的右侧;偏度大于0表示为右偏(正偏态),绝大多数值位于平均值的左侧;偏度为0表示数据关于均值对称分布。峰度体现数据分布的陡峭程度,峰度小于0表示为低峰态,即数据分布比较分散;峰度大于0为尖峰态,即数据分布比较集中。理想正态分布的偏度和峰度系数都为0,偏度和峰度系数绝对值越小,表示数据分布越接近于正态分布。
-
利用Shapiro-Wilk法对各样地各林层的直径分布进行正态性检验,其统计假设为 H0:样本来自正态分布的总体;H1:样本来自非正态分布的总体。在利用该方法进行检验时,首先将样本按大小值升序排列,然后计算统计量W,将计算统计量W与临界值
${W_{\alpha [n]}}$ 比较,若计算值小于临界值,则拒绝原假设H0。统计量W计算公式如下:$W = \frac{{{{\left\{ {\displaystyle\sum\limits_{i = 1}^{\left[ {\frac{n}{2}} \right]} {{a_i}(W)[{x_{n + 1 - i}} - {x_i}]} } \right\}}^2}}}{{\displaystyle\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} }}$
(1) 式中:n为样本量,
$\bar x$ 表示样本均值;${a_i}(W)$ 可查表获得;$\left[ {\dfrac{n}{2}} \right]$ 表示数n/2的整数部分。 -
选用Weibull分布和Meyer负指数函数拟合各林层直径分布,各分布函数计算公式如下:
(1)Weibull分布密度函数
$ f(x)=\left\{\begin{array}{l}0, x\le a;\\ \dfrac{c}{b}{\left(\dfrac{x-a}{b}\right)}^{c-1}*\exp\left[-{\left(\dfrac{x-a}{b}\right)}^{c}\right],\;\;\;x > a,b > 0,c > 0{\text{。}}\end{array}\right.$
(2) 式中:a为位置参数,b为尺度参数,c为形状参数。
(2)Meyer负指数函数
$Y = K{e^{ - ax}}$
(3) 式中:Y为每个径阶的林木株数;x为径阶;e为自然对数的底;a,K为直径分布特征的常数。
-
根据不同分布函数求得的理论株数,计算卡方检验值χ2作为不同分布函数拟合效果的检验标准。χ2值计算公式如下:
${\chi ^2}{\rm{ = }}\sum\limits_{i = 1}^m {\frac{{{{({n_i} - {{\hat n}_i})}^2}}}{{{{\hat n}_i}}}} $
(4) 式中:m为径阶数;ni为第i径阶实际株数;
${\hat n_i}$ 为第i径阶理论株数;χ2自由度为m−k−1,k为参数个数。 -
计算各样地各林层的偏度和峰度值,并进行正态性检验,结果见表1。从S-W检验结果来看,各样地全林的P值均小于0.05,说明其直径分布均不服从正态分布,这与典型人工林的直径分布有显著区别;所有样地的第Ⅱ亚层均未通过正态性检验,第Ⅰ亚层中有5块样地服从正态分布。
表 1 各样地各林层直径分布特征值
Table 1. Characteristic values of diameter distributions for each sample plot and storey
样地号
Plot No.层属
Storey偏度系数
SK峰度系数
KTS-W检验P值
P value of S-W test1 全林 Stand 0.60 −0.70 0.000 第Ⅰ亚层
Sublayer Ⅰ0.15 −0.75 0.078* 第Ⅱ亚层
Sublayer Ⅱ0.83 −0.13 0.000 2 全林 Stand 0.77 0.02 0.000 第Ⅰ亚层
Sublayer Ⅰ0.60 −0.13 0.001 第Ⅱ亚层
Sublayer Ⅱ0.76 −0.48 0.000 3 全林 Stand 0.59 −0.51 0.000 第Ⅰ亚层
Sublayer Ⅰ0.44 −0.43 0.010 第Ⅱ亚层
Sublayer Ⅱ1.09 0.81 0.000 4 全林 Stand 0.77 −0.41 0.000 第Ⅰ亚层
Sublayer Ⅰ0.05 −0.77 0.186* 第Ⅱ亚层
Sublayer Ⅱ0.78 −0.18 0.000 5 全林 Stand 0.91 0.01 0.000 第Ⅰ亚层
Sublayer Ⅰ0.25 −0.51 0.366* 第Ⅱ亚层
Sublayer Ⅱ1.05 0.69 0.000 6 全林 Stand 0.55 −0.56 0.000 第Ⅰ亚层
Sublayer Ⅰ0.36 −0.69 0.009 第Ⅱ亚层
Sublayer Ⅱ0.88 0.04 0.000 7 全林 Stand 0.55 −0.55 0.000 第Ⅰ亚层
Sublayer Ⅰ0.30 −0.36 0.181* 第Ⅱ亚层
Sublayer Ⅱ1.11 0.72 0.000 8 全林 Stand 0.48 −0.49 0.000 第Ⅰ亚层
Sublayer Ⅰ0.50 −0.49 0.001 第Ⅱ亚层
Sublayer Ⅱ1.05 0.72 0.000 9 全林 Stand 0.54 −0.42 0.000 第Ⅰ亚层
Sublayer Ⅰ0.34 0.01 0.352* 第Ⅱ亚层
Sublayer Ⅱ1.06 0.43 0.000 10 全林 Stand 1.05 0.95 0.000 第Ⅰ亚层
Sublayer Ⅰ0.71 0.26 0.005 第Ⅱ亚层
Sublayer Ⅱ0.94 0.50 0.000 *表示服从假设分布。
* Means obeying the hypothesis distribution.分析林分及各亚层的偏度系数可知,所有样地各林层的偏度系数均为正值,说明直径分布曲线均为右偏,林分或亚层内小于平均直径的林木株数较多,直径偏向小径阶;所有样地第Ⅱ亚层的偏度系数均大于第Ⅰ亚层,说明相对于第Ⅱ亚层来说第Ⅰ亚层的直径分布更接近于正态分布;比较各样地全林及各亚层的偏度系数可知,除2号、8号和10号样地外,其余样地的全林偏度系数均介于第Ⅰ亚层和第Ⅱ亚层之间。
从峰度系数来看,全林中除2号、5号和10号样地的峰度大于0外,其余样地的峰度均小于0,说明大多数样地的分布曲线呈低峰态,直径分布比较分散;除1号、4号和6号样地外,其余样地第Ⅱ亚层的峰度绝对值均大于第Ⅰ亚层峰度绝对值;比较各样地全林及各亚层的峰度系数可知,除2号、5号和10号样地外,其余样地的全林峰度系数绝对值均介于第Ⅰ亚层和第Ⅱ亚层峰度绝对值之间。
-
利用χ2检验法在0.05的显著性水平下对各样地各林层的直径分布拟合结果进行检验,若χ2 < χ20.05则说明在0.05水平下拟合效果显著,Weibull分布、Meyer负指数分布的拟合参数及卡方检验结果见表2。
表 2 各样地各林层直径分布拟合参数值及检验结果
Table 2. The fitting parameters and inspection results of diameter distributions for each sample plot and storey
样地号
Plot No.层属
StoreyWeibull分布 Meyer负指数函数 参数
Parameters卡方值
Chi-square value参数
Parameters卡方值
Chi-square valuea b c χ2 χ20.05 K a χ2 χ20.05 1 全林 Stand 5.999 10.064 0.994 5.092* 12.592 107.033 0.107 5.186* 14.067 第Ⅰ亚层 Sublayer Ⅰ 5.279 11.611 2.360 2.175* 12.592 13.218 −0.004 37.681 14.067 第Ⅱ亚层 Sublayer Ⅱ 5.000 3.003 1.219 0.835* 3.841 358.938 0.301 0.939* 3.841 2 全林 Stand 4.348 8.644 1.393 7.760* 14.067 77.678 0.089 17.910 15.507 第Ⅰ亚层 Sublayer Ⅰ 5.645 9.608 11.201 11.201* 14.067 22.946 0.031 58.200 15.507 第Ⅱ亚层 Sublayer Ⅱ 5.187 3.335 1.056 2.000* 3.841 211.086 0.289 2.419* 5.991 3 全林 Stand 5.208 9.649 1.145 10.865* 15.507 63.865 0.082 15.159* 16.919 第Ⅰ亚层 Sublayer Ⅰ 6.000 10.804 2.150 4.636* 15.507 15.906 0.019 60.845 16.919 第Ⅱ亚层 Sublayer Ⅱ 4.908 3.124 1.310 4.696 3.841 229.297 0.299 5.467* 5.991 4 全林 Stand 5.997 11.382 0.947 9.249* 16.919 75.020 0.125 11.194* 18.307 第Ⅰ亚层 Sublayer Ⅰ 5.000 14.062 1.807 15.154* 16.919 10.603 0.029 15.553* 18.307 第Ⅱ亚层 Sublayer Ⅱ 5.502 4.230 0.953 3.086* 3.841 145.589 0.254 3.369* 5.991 5 全林 Stand 5..433 7.593 1.012 5.479* 14.067 100.005 0.129 4.434* 15.507 第Ⅰ亚层 Sublayer Ⅰ 4.402 12.627 2.250 5.364* 14.067 9.673 0.012 22.719 15.507 第Ⅱ亚层 Sublayer Ⅱ 4.747 3.534 1.424 0.559* 5.991 211.021 0.259 6.183* 7.815 6 全林 Stand 5.998 10.647 0.999 16.035 12.592 63.324 0.084 12.981* 14.067 第Ⅰ亚层 Sublayer Ⅰ 5.780 10.646 2.068 9.355* 12.592 12.457 0.002 36.115 14.067 第Ⅱ亚层 Sublayer Ⅱ 5.237 3.394 0.958 4.391* 5.991 231.060 0.303 3.512* 7.815 7 全林 Stand 5.973 9.654 1.010 12.566* 12.592 83.482 0.091 12.032* 14.067 第Ⅰ亚层 Sublayer Ⅰ 5.999 10.196 2.427 5.311* 12.592 13.670 −0.001 54.500 14.067 第Ⅱ亚层 Sublayer Ⅱ 4.611 3.288 1.467 5.254* 5.991 283.565 0.292 5.827* 7.815 8 全林 Stand 3.745 9.491 1.500 12.079* 12.592 69.279 0.077 17.254 14.067 第Ⅰ亚层 Sublayer Ⅰ 7.663 8.228 1.762 4.029* 11.071 26.525 0.033 36.942 12.592 第Ⅱ亚层 Sublayer Ⅱ 5.381 3.857 0.882 5.103* 5.991 247.803 0.293 4.776* 7.815 9 全林 Stand 5.999 11.708 0.994 19.511 15.507 71.481 0.090 17.313 16.919 第Ⅰ亚层 Sublayer Ⅰ 5.297 11.720 2.535 5.366* 15.507 13.872 0.017 59.709 16.919 第Ⅱ亚层 Sublayer Ⅱ 5.280 3.511 0.909 5.000* 5.991 270.918 0.306 5.936* 7.815 10 全林 Stand 4.859 7.450 1.274 7.078* 15.507 80.561 0.111 15.351* 16.919 第Ⅰ亚层 Sublayer Ⅰ 3.214 12.357 2.738 13.140* 15.507 11.831 0.032 30.008 16.919 第Ⅱ亚层 Sublayer Ⅱ 4.905 4.499 1.305 2.752* 7.815 115.074 0.191 6.619* 9.488 *表示服从假设分布。
* Means obeying the hypothesis distribution.由表2可知,对于Weibull分布而言,10块样地的全林直径分布中,只有6号和9号样地未通过卡方检验,其余8块样地均通过检验;所有样地的第Ⅰ亚层直径分布均服从Weibull分布,第Ⅱ亚层中仅有3号样地未通过。对于Meyer负指数分布而言,10块样地的全林直径分布中,有3块样地未通过,通过率较Weibull分布更低;10块样地中仅有4号样地的第Ⅰ亚层直径分布服从Meyer负指数分布,其余9块样地均拒绝;但对于各样地第Ⅱ亚层来说,Meyer负指数分布的通过率高达100%。总体而言,Weibull分布在全林及第Ⅰ亚层的拟合效果更好,特别是对于第Ⅰ亚层的拟合效果显著,而Meyer负指数分布则能更好的拟合第Ⅱ亚层直径分布。
-
通过比较两种分布函数的拟合效果,选择Weibull分布拟合各样地全林及第Ⅰ亚层的直径分布,第Ⅱ亚层则选用Meyer负指数分布进行拟合,结果见图1、图2。

图 1 1~5号样地直径分布和分布函数拟合
Figure 1. Line charts of diameter class and fitting curves of distribution functions of No.1~5 sample plots
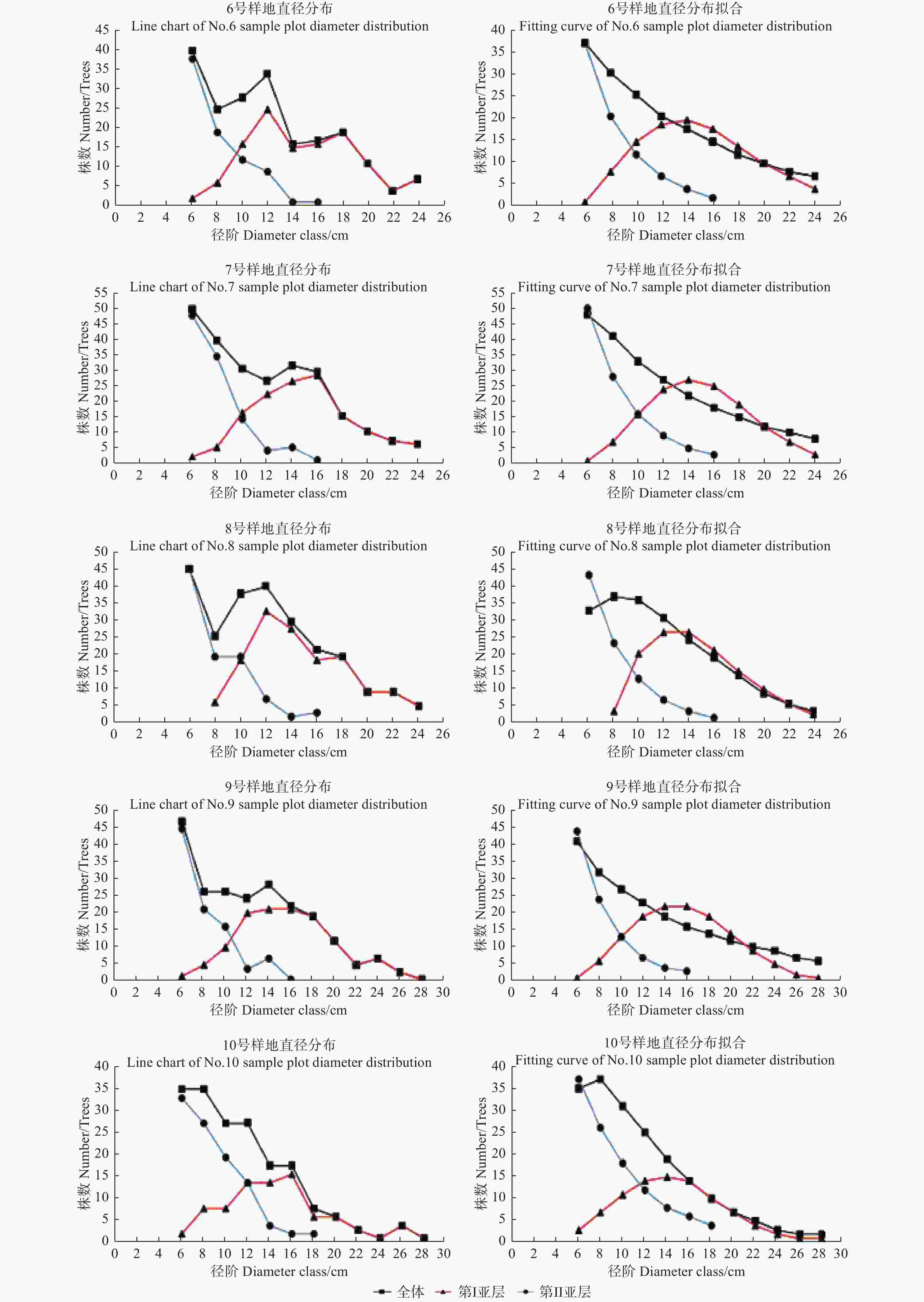
图 2 6~10号样地直径分布和分布函数拟合
Figure 2. Line charts of diameter class and fitting curves of distribution functions of No.6~10 sample plots
从图1、图2可以看出,全林直径分布呈反J型或波纹状反J型曲线,第Ⅰ亚层和第Ⅱ亚层的直径分布差异显著,但各样地的各对应亚层表现相对一致,整体表现为第Ⅰ亚层呈山状曲线或多峰分布,第Ⅱ亚层则呈反J型;从第Ⅱ亚层过渡到第Ⅰ亚层时,亚层直径分布在图上表现为顶峰右移、峰值减小。各样地的第Ⅰ亚层直径分布与全林直径分布均有重叠,重叠部分的起始径阶介于14~18 cm之间,但第Ⅱ亚层直径分布与全林直径分布基本没有重叠。各样地第Ⅰ亚层与第Ⅱ亚层均存在交点,交点径阶介于8~14 cm之间,在该径阶范围内相同直径大小的林木处于第Ⅰ亚层与第Ⅱ亚层的株数大致相等,说明该径阶范围内林分的树高结构比较复杂,可能对林分树高研究产生影响。
-
对半天然马尾松阔叶混交林进行林层划分后,各亚层S-W检验显著度随亚层高度升高而增大,偏度和峰度系数则随之减小,说明第Ⅰ亚层较第Ⅱ亚层更趋向于正态分布,这与庄崇洋等[9]对典型中亚热带天然阔叶林林层直径分布规律的研究结果类似。
为研究复层异龄混交林的直径结构规律,前苏联特烈其亚科夫提出“森林分子”学说,将同一立地条件下生长发育起来的同一树种同一年龄世代和同一起源的林木视为一个森林分子,随后的研究及大量检验表明,将复杂林分划分为森林分子后,在每个森林分子内部都存在与同龄林一致的结构规律[20,26]。本研究中的半天然马尾松阔叶混交林本质上是复层异龄混交林,在划分林层后,马尾松均集中在第Ⅰ亚层(各样地第Ⅱ亚层内马尾松株数最多为4株,株数占比为5%),将各样地第Ⅰ亚层的马尾松视为1个森林分子,对其进行正态检验,结果表明仅有4块样地服从正态分布。加入第Ⅱ亚层的马尾松后,检验结果亦然。从理论上来说,各样地内马尾松森林分子的直径结构应表现出同龄人工纯林的直径分布特征,即服从正态分布,但检验结果并非如此,导致这种结果的原因可能有以下几点:第一,持续进入的天然更新阔叶树数量较多、树种组成多样、各树种种群分布格局各异,天然更新阔叶树与马尾松之间产生了激烈的竞争,不仅对马尾松生长空间造成挤压,而且由于对光的竞争可能会迫使马尾松将更多的物质与能量用于高生长;第二,从林分内天然更新阔叶树的直径结构可以推测,天然更新阔叶树的进入是一个持续不断的过程,对马尾松生长的干扰是持续的;第三,林分年龄较小、密度大,林内小径阶林木居多且以天然更新阔叶树为主,林分尚处于林木竞争激烈、林分状态不稳定的阶段。
-
(1)半天然马尾松阔叶混交林全林和第Ⅱ亚层均不服从正态分布,全林直径分布呈反J型或波纹状反J型曲线,第Ⅱ亚层的直径分布呈反J型,第Ⅰ亚层为倾向于正态分布的山状曲线或多峰分布,林层间直径分布差异显著,分林层研究林分直径分布是有必要的。
(2)全林峰度和偏度系数绝对值介于第Ⅰ亚层和第Ⅱ亚层之间,S-W检验的P值均表现为第Ⅰ亚层大于第Ⅱ亚层,峰度和偏度系数绝对值表现为第Ⅰ亚层小于第Ⅱ亚层,从第Ⅱ亚层过渡到第Ⅰ亚层时,在直径分布图上表现为顶峰右移、峰值下降,从第Ⅱ亚层到第Ⅰ亚层直径分布表现出由负指数分布向正态分布过渡的趋势。
(3) Weibull分布和Meyer负指数分布均取得较好的拟合效果,Weibull分布对全林和第Ⅰ亚层的拟合效果更好,Meyer负指数分布更适合拟合第Ⅱ亚层直径分布。
基于分层的半天然马尾松阔叶混交林直径分布
Diameter Distribution of Semi-natural Mixed Forest of Pinus massoniana and Broadleaved Trees Based on Stratification
-
摘要:
目的 研究半天然马尾松阔叶混交林各林层(包括全林和各亚层)的直径分布,揭示其直径分布特征,为其可持续经营提供基础依据。 方法 基于10块半天然马尾松阔叶混交林样地,采用最大受光面法划分林层,利用Shapiro-Wilk检验对各样地各林层直径分布进行正态性检验,利用峰度和偏度系数描述直径分布图形特征,采用三参数Weibull分布和Meyer负指数函数拟合各样地各林层直径分布,用卡方检验法检验拟合效果,并选择效果较好的函数拟合各样地直径分布图,分析林分直径分布特征。 结果 有5块样地的第Ⅰ亚层服从正态分布,但所有样地全林和第Ⅱ亚层的直径分布均呈反J形且不服从正态分布。所有样地全林和各亚层的偏度系数均为正值,有7块样地的全林峰度系数小于0,大多数样地全林的偏度系数及峰度系数绝对值介于第Ⅰ亚层和第Ⅱ亚层之间。Weibull分布函数对全林和第Ⅰ亚层的拟合效果较好,全林、第Ⅰ亚层、第Ⅱ亚层的卡方检验通过率分别为80%、100%、70%;Meyer负指数函数对第Ⅱ亚层的拟合效果较好,而对全林和第Ⅰ亚层的适应性较差,特别是第Ⅰ亚层的通过率仅为10%,但第Ⅱ亚层的通过率达100%。 结论 半天然马尾松阔叶混交林各林层的直径分布差异显著,第Ⅰ亚层倾向于正态分布,全林和第Ⅱ亚层的直径分布均呈反J 形且都不服从正态分布;从第Ⅱ亚层到第Ⅰ亚层直径分布表现出由负指数分布向正态分布过渡的趋势。所有样地各林层的直径分布曲线均为右偏,大多数样地的全林直径分布曲线呈低峰态。Weibull分布函数对全林和第Ⅰ亚层的拟合效果较好,而Meyer负指数函数则适用于拟合第Ⅱ亚层直径分布。 Abstract:Objective The diameter distribution of each storey (including the whole stand and sublayers) of semi-natural mixed forest of Pinus massoniana and broadleaved trees was studied to reveal the diameter distribution characteristics of the stand and provide data for their sustainable management. Method Based on 10 semi-natural mixed forests plots, the maximum light-receiving plane method was used to divide storey, and the Shapiro-Wilk test was used to measure the normality of the diameter distribution of each plot and storey; the skewness and kurtosis coefficients were used to describe the graphic characteristics of the diameter distribution. The diameter distributions of each plot and storey were fitted by three-parameter Weibull distribution and the Meyer negative exponential function, and the chi-square test was used to test the fitting effect, then the function with better fitting effects was selected to fit the distribution chart of each plot, and analyzed the distribution characteristics of the stand. Result There were five plots whose sublayer Ⅰ obeyed normal distribution, but for all sample plots, the diameter distribution of all the whole stand and the sublayer Ⅱ followed an inversed J shape were not obeying normal distribution. The skewness coefficient of all the whole stand and sublayers were positive value, the kurtosis coefficient of the whole stand of 7 plots were less than 0, and for most plots the skewness coefficient and the absolute value of the kurtosis coefficient of the whole stand were between that values of the sublayer Ⅰ and the sublayer Ⅱ. The Weibull distribution function has a good fitting effect on the whole stand and the sublayer Ⅰ. The pass rates of the chi-square test of the whole stand, the sublayer Ⅰ and the sublayer Ⅱ were 80%, 100%, and 70%, respectively. Meyer negative exponential function could fit the sublayer Ⅱ better, while the adaptability to the whole stand and the sublayer Ⅰ were poor, especially the pass rate of the sublayer Ⅰ was only 10%, but the pass rate of the sublayer Ⅱ reached 100%. Conclusion There are significant differences in the diameter distribution of the whole stand and each sublayer of the semi-natural mixed forest of P. massoniana and broadleaved trees, the diameter distribution of sublayer Ⅰ tends to be normal distribution while the whole stand and the sublayer Ⅱ are inverse J shaped and not obeying normal distribution. The diameter distribution from sublayer Ⅱ to sublayer Ⅰ shows a transition trend from negative exponential distribution to normal distribution. For all sample plots, the diameter distribution curves of each storey are right-skewed, and the curves of the whole stand of most sample plots are platykurtic. The Weibull distribution function has a good fitting effect on the whole stand and the sublayer Ⅰ, while the Meyer negative exponential function is suitable for fitting diameter distribution of sublayer Ⅱ. -
表 1 各样地各林层直径分布特征值
Table 1. Characteristic values of diameter distributions for each sample plot and storey
样地号
Plot No.层属
Storey偏度系数
SK峰度系数
KTS-W检验P值
P value of S-W test1 全林 Stand 0.60 −0.70 0.000 第Ⅰ亚层
Sublayer Ⅰ0.15 −0.75 0.078* 第Ⅱ亚层
Sublayer Ⅱ0.83 −0.13 0.000 2 全林 Stand 0.77 0.02 0.000 第Ⅰ亚层
Sublayer Ⅰ0.60 −0.13 0.001 第Ⅱ亚层
Sublayer Ⅱ0.76 −0.48 0.000 3 全林 Stand 0.59 −0.51 0.000 第Ⅰ亚层
Sublayer Ⅰ0.44 −0.43 0.010 第Ⅱ亚层
Sublayer Ⅱ1.09 0.81 0.000 4 全林 Stand 0.77 −0.41 0.000 第Ⅰ亚层
Sublayer Ⅰ0.05 −0.77 0.186* 第Ⅱ亚层
Sublayer Ⅱ0.78 −0.18 0.000 5 全林 Stand 0.91 0.01 0.000 第Ⅰ亚层
Sublayer Ⅰ0.25 −0.51 0.366* 第Ⅱ亚层
Sublayer Ⅱ1.05 0.69 0.000 6 全林 Stand 0.55 −0.56 0.000 第Ⅰ亚层
Sublayer Ⅰ0.36 −0.69 0.009 第Ⅱ亚层
Sublayer Ⅱ0.88 0.04 0.000 7 全林 Stand 0.55 −0.55 0.000 第Ⅰ亚层
Sublayer Ⅰ0.30 −0.36 0.181* 第Ⅱ亚层
Sublayer Ⅱ1.11 0.72 0.000 8 全林 Stand 0.48 −0.49 0.000 第Ⅰ亚层
Sublayer Ⅰ0.50 −0.49 0.001 第Ⅱ亚层
Sublayer Ⅱ1.05 0.72 0.000 9 全林 Stand 0.54 −0.42 0.000 第Ⅰ亚层
Sublayer Ⅰ0.34 0.01 0.352* 第Ⅱ亚层
Sublayer Ⅱ1.06 0.43 0.000 10 全林 Stand 1.05 0.95 0.000 第Ⅰ亚层
Sublayer Ⅰ0.71 0.26 0.005 第Ⅱ亚层
Sublayer Ⅱ0.94 0.50 0.000 *表示服从假设分布。
* Means obeying the hypothesis distribution.表 2 各样地各林层直径分布拟合参数值及检验结果
Table 2. The fitting parameters and inspection results of diameter distributions for each sample plot and storey
样地号
Plot No.层属
StoreyWeibull分布 Meyer负指数函数 参数
Parameters卡方值
Chi-square value参数
Parameters卡方值
Chi-square valuea b c χ2 χ20.05 K a χ2 χ20.05 1 全林 Stand 5.999 10.064 0.994 5.092* 12.592 107.033 0.107 5.186* 14.067 第Ⅰ亚层 Sublayer Ⅰ 5.279 11.611 2.360 2.175* 12.592 13.218 −0.004 37.681 14.067 第Ⅱ亚层 Sublayer Ⅱ 5.000 3.003 1.219 0.835* 3.841 358.938 0.301 0.939* 3.841 2 全林 Stand 4.348 8.644 1.393 7.760* 14.067 77.678 0.089 17.910 15.507 第Ⅰ亚层 Sublayer Ⅰ 5.645 9.608 11.201 11.201* 14.067 22.946 0.031 58.200 15.507 第Ⅱ亚层 Sublayer Ⅱ 5.187 3.335 1.056 2.000* 3.841 211.086 0.289 2.419* 5.991 3 全林 Stand 5.208 9.649 1.145 10.865* 15.507 63.865 0.082 15.159* 16.919 第Ⅰ亚层 Sublayer Ⅰ 6.000 10.804 2.150 4.636* 15.507 15.906 0.019 60.845 16.919 第Ⅱ亚层 Sublayer Ⅱ 4.908 3.124 1.310 4.696 3.841 229.297 0.299 5.467* 5.991 4 全林 Stand 5.997 11.382 0.947 9.249* 16.919 75.020 0.125 11.194* 18.307 第Ⅰ亚层 Sublayer Ⅰ 5.000 14.062 1.807 15.154* 16.919 10.603 0.029 15.553* 18.307 第Ⅱ亚层 Sublayer Ⅱ 5.502 4.230 0.953 3.086* 3.841 145.589 0.254 3.369* 5.991 5 全林 Stand 5..433 7.593 1.012 5.479* 14.067 100.005 0.129 4.434* 15.507 第Ⅰ亚层 Sublayer Ⅰ 4.402 12.627 2.250 5.364* 14.067 9.673 0.012 22.719 15.507 第Ⅱ亚层 Sublayer Ⅱ 4.747 3.534 1.424 0.559* 5.991 211.021 0.259 6.183* 7.815 6 全林 Stand 5.998 10.647 0.999 16.035 12.592 63.324 0.084 12.981* 14.067 第Ⅰ亚层 Sublayer Ⅰ 5.780 10.646 2.068 9.355* 12.592 12.457 0.002 36.115 14.067 第Ⅱ亚层 Sublayer Ⅱ 5.237 3.394 0.958 4.391* 5.991 231.060 0.303 3.512* 7.815 7 全林 Stand 5.973 9.654 1.010 12.566* 12.592 83.482 0.091 12.032* 14.067 第Ⅰ亚层 Sublayer Ⅰ 5.999 10.196 2.427 5.311* 12.592 13.670 −0.001 54.500 14.067 第Ⅱ亚层 Sublayer Ⅱ 4.611 3.288 1.467 5.254* 5.991 283.565 0.292 5.827* 7.815 8 全林 Stand 3.745 9.491 1.500 12.079* 12.592 69.279 0.077 17.254 14.067 第Ⅰ亚层 Sublayer Ⅰ 7.663 8.228 1.762 4.029* 11.071 26.525 0.033 36.942 12.592 第Ⅱ亚层 Sublayer Ⅱ 5.381 3.857 0.882 5.103* 5.991 247.803 0.293 4.776* 7.815 9 全林 Stand 5.999 11.708 0.994 19.511 15.507 71.481 0.090 17.313 16.919 第Ⅰ亚层 Sublayer Ⅰ 5.297 11.720 2.535 5.366* 15.507 13.872 0.017 59.709 16.919 第Ⅱ亚层 Sublayer Ⅱ 5.280 3.511 0.909 5.000* 5.991 270.918 0.306 5.936* 7.815 10 全林 Stand 4.859 7.450 1.274 7.078* 15.507 80.561 0.111 15.351* 16.919 第Ⅰ亚层 Sublayer Ⅰ 3.214 12.357 2.738 13.140* 15.507 11.831 0.032 30.008 16.919 第Ⅱ亚层 Sublayer Ⅱ 4.905 4.499 1.305 2.752* 7.815 115.074 0.191 6.619* 9.488 *表示服从假设分布。
* Means obeying the hypothesis distribution. -
[1] 王 蒙, 李凤日. 基于抚育间伐效应的落叶松人工林直径分布动态模拟[J]. 应用生态学报, 2016, 27(8):2429-2437. [2] Cheng C P, Wei C, Tsai M J, et al. A Weibull model of the impact of thinning and a typhoon event on the stand structure of Cryptomeria japonica in Central Taiwan over 100 years[J]. Journal of Forest Research, 2017, 22(1): 22-29. doi: 10.1080/13416979.2016.1256550 [3] 周国强, 陈彩虹, 楚春晖, 等. 大围山杉木人工林不同海拔直径分布研究[J]. 西北林学院学报, 2017, 32(1):86-91. doi: 10.3969/j.issn.1001-7461.2017.01.14 [4] 周泽宇, 杨绕华, 张玉珍, 等. 华北落叶松人工林直径分布预测模型构建[J]. 南京林业大学学报: 自然科学版, 2020, 44(2):117-124. [5] 张 鹏, 王新杰, 许 昊. 杉木幼龄林直径分布[J]. 东北林业大学学报, 2014, 42(11):7-10, 13. doi: 10.3969/j.issn.1000-5382.2014.11.002 [6] Tatiana V, Tzvetan M. Modeling diameter distribution of Austrian black pine (Pinus nigra Arn.) plantations: a comparison of the Weibull frequency distribution function and percentile-based projection methods[J]. European Journal of Forest Research, 2010, 129(6): 1169-1179. doi: 10.1007/s10342-010-0407-y [7] 王千雪, 万 盼, 刘 灵, 等. 兴安落叶松天然林林木直径与树高分布的分层特征[J]. 林业科学研究, 2018, 31(5):82-90. [8] Knoke T, Plusczyk N. On economic consequences of transformation of a spruce (Picea abies (L.) Karst.) dominated stand from regular into irregular age structure[J]. Forest Ecology and Management, 2001, 151(1/3): 163-179. [9] 庄崇洋, 黄清麟, 马志波, 等. 典型中亚热带天然阔叶林各林层直径分布及其变化规律[J]. 林业科学, 2017, 53(4):18-27. doi: 10.11707/j.1001-7488.20170403 [10] 许彦红, 杨宇明, 杜 凡, 等. 西双版纳热带雨林林分直径结构研究[J]. 西南林学院学报, 2004, 24(2):16-18. [11] FAO. Proceedings: second expert meeting on harmonizing forest-related definitions for use by various stakeholders[C]. Rome: Publications Division of FAO. [12] 王金池, 黄清麟, 马志波, 等. 永安市半天然马尾松阔叶混交林的树种组成与多样性[J]. 林业科学, 2019, 55(11):19-26. doi: 10.11707/j.1001-7488.20191103 [13] 陈存及, 董建文, 林敬德, 等. 半天然杉阔混交林分形成, 发育与结构特征[J]. 福建林学院学报, 1996, 16(4):310-314. [14] 陈存及, 陈新芳, 董建文, 等. 半天然杉阔混交林优势种群的增长规律[J]. 热带亚热带植物学报, 2002, 10(3):253-257. doi: 10.3969/j.issn.1005-3395.2002.03.011 [15] 杨 梅, 林思祖, 曹光球, 等. 不同生境杉木马尾松半天然混交林物种多样性分析[J]. 安徽农业科学, 2008, 36(33):14521-14523. doi: 10.3969/j.issn.0517-6611.2008.33.068 [16] 曹光球, 林思祖, 曹子林, 等. 半天然杉阔混交林杉木及其伴生树种种群空间格局[J]. 浙江林学院学报, 2002, 19(2):148-152. [17] 庄树宏, 王克明, 陈礼学. 昆嵛山老杨坟阳坡与阴坡半天然植被植物群落生态学特性的初步研究[J]. 植物生态学报, 1999, 23(3):47-58. [18] 张会儒, 李春明, 武纪成. 金沟岭天然和半天然混交林林分空间结构比较[J]. 科技导报, 2009, 27(19):79-84. doi: 10.3321/j.issn:1000-7857.2009.19.019 [19] 庄崇洋, 黄清麟, 马志波, 等. 中亚热带天然阔叶林林层划分新方法——最大受光面法[J]. 林业科学, 2017, 53(3):1-11. doi: 10.11707/j.1001-7488.20170301 [20] 陈昌雄, 陈平留, 刘 健, 等. 闽北天然次生林林木直径分布规律的研究[J]. 福建林学院学报, 1996, 16(2):122-125. [21] 徐 允. 东北地区天然次生林主要林分类型直径分布的研究[D]. 哈尔滨: 东北林业大学, 2012. [22] 赵 娜, 郑小贤. 福建将乐林场栲属次生林直径结构的研究[J]. 中南林业科技大学学报, 2014, 34(2):77-80. [23] 郝文乾, 陈 玲, 梅光义. 杉木人工林直径分布的坡向效应及其模拟[J]. 西北农林科技大学学报: 自然科学版, 2016, 44(11):61-69. [24] 张梦弢, 亢新刚, 郭韦韦, 等. 长白山云冷杉混交林直径结构分布研究[J]. 西北农林科技大学学报: 自然科学版, 2015, 43(9):65-72. [25] 褚 欣, 潘 萍, 李 琦, 等. 闽楠天然次生林直径分布模拟研究[J]. 江西农业大学学报, 2019, 41(2):273-280. [26] 孟宪宇. 测树学[M]. 北京: 中国林业出版社, 2006. -



 下载:
下载:











