-
树高是估测森林生长与收获、预测地位指数和研究森林垂直结构的重要特征因子之一[1]。胸径和树高之间有很强的相关性,而胸径简单易测且测量准确,所以建立树高-胸径模型,利用胸径预测树高方便且实用[2]。树高生长还受到立地条件和林分年龄等多种因素的影响[3],研究表明加入林分断面积、立地指数、林分平均高或林分年龄等林分特征因子,建立的广义胸径-树高模型能够用于不同林分的树高预测[4-5]。过去的研究多是依据前人经验选择若干个不同形式的基础模型,然后通过非线性回归拟合求参,选出精度最高的模型用于研究区树高的预测[6]。但是,研究者需要尝试各种模型形式,经过大量的分析比较才能得到精度较高的模型,耗时且低效[7]。而且不同的研究者选择基础模型的数量和种类有所不同,会导致研究结果产生较大差异[8]。另一种应用广泛的基于非线性混合效应建立树高-胸径模型,该类模型具有良好的预测能力[9],但是由于随机参数的引入,使模型结构变得更加复杂,增加了建模难度,会出现模型难以收敛的情况[10]。此外,传统的建模方法都受到统计学假设的局限,如:胸径-树高数据通常是来自同一林分的多个样地,或者是相同样地的连续测量,导致数据结构违背了独立分布的假设条件[11]。
随着计算机技术的发展与更新,人工智能为模型构建提供了先进的思路和手段,能够在一定程度上克服上述问题。人工神经网络是人工智能的一个分支,它对数据分布没有假设要求,能很好地处理非线性、非高斯分布和包含噪声的低质量数据[12],而且建模前不需要明确模型具体形式,非常适宜处理复杂的多变量、非线性问题,已经在预测林木胸径、材积和林分蓄积、生物量[12-14]方面有所研究。特别是BP-ANN,应用更为广泛,卯光宪用以建立马尾松树高-胸径模型[8],刘鑫用以建立云冷杉混交林中不同树种的树高-胸径模型[7],均表明ANN模型的精度高于传统模型,具有泛化能力强、高效低偏的优点。
但是这些研究都是基于单层神经网络,而树高生长具有连续性和相关性,树高-胸径的关系受到各种相关因素影响,单层的网络结构不足以模拟这种复杂的非线性结构[15]。深度学习(DLA)模型是人工神经网络的一个分支,兴起于2010年,是近年来研究的热点,DLA模型包含3层及以上的隐藏层和更多的神经元,其复杂的结构更接近人脑,具有自学习和自决策的能力,被认为是比单层神经网络更为合适的建模方法[15-16]。目前在语音、图像识别、生物医学和人工智能等领域开始有所应用[17],在林业领域也有采用深度学习预测森林火灾,或对遥感影像进行单木冠幅分割的研究[18-19]。迄今为止,国内基于深度学习构建森林模型、预测单木或林分参数的研究尚不多见,也未有基于深度学习建立树高-胸径模型的文献。
本研究以福建省将乐国有林场的杉木为对象,基于H2O平台的深度学习算法,建立多个胸径-树高DLA模型,探讨深度学习在林业建模方面的可行性。同时基于传统非线性回归建立10个广义树高-胸径模型,筛选精度最高者作为对照。以期探索一种更高效低偏的树高预测方法,同时确定最优的树高-胸径DLA模型形式,为研究区森林资源监测和评价提供参考。
-
研究区位于福建省将乐国有林场(117°05′~117°40′ E,26°26′~27°04′ N),地处福建省西北部的三明市将乐县。属于亚热带季风气候,温暖湿润,四季分明。年平均温度18.6 ℃,年平均降水1 721.6 mm。地形以中低山为主,海拔约为400~800 m,土层深厚,土壤肥沃。分布主要乔木有杉木(Cunninghamia lanceolata (Lamb.) Hook.)、毛竹(Phyllostachys heterocycla Carr.)和马尾松(Pinus massoniana Lamb.)等。
-
在研究区内选择不同林龄的杉木人工林,共设置34块标准地,进行每木检尺,起测径阶为4 cm,测量树高(H)和胸径(D),并计算平均胸径(Dg)。然后在每块标准地内选取3~5株优势木,以其平均胸径和平均树高分别作为优势树高(Ht)和优势胸径(Dt)。最后,剔除枯死木和缺失值,共得到2 989组杉木的胸径-树高数据,选取其中的25块样地(2 253组)作为建模数据集,剩余9块(645组)为检验数据集。统计因子见表1。
表 1 建模数据和见证数据统计
Table 1. Summary statistics of modeling set and validation set
测树因子
Statistics建模数据 Train set 检验数据 Validation set 最小值 Min 最大值 Max 平均值 Mean 标准差 sd 最小值 Min 最大值 Max 平均值 Mean 标准差 sd 胸径 D/cm 3.9 43.5 16.4 7.18 4.4 44.5 16.6 7.59 树高 H/m 2.9 30.5 14.5 5.46 4.5 27.8 14.9 6.14 优势胸径 Dt/cm 14.9 39.9 26.6 6.24 14.9 39.9 26.6 5.73 优势树高 Ht/m 11.3 30.5 22.1 4.80 11.3 30.5 22.3 4.69 平均胸径 Dg/cm 9.9 28.1 17.2 4.91 9.9 28.1 17.4 5.04 -
根据以往研究,选择10个已经被广泛使用且精度较高的广义树高-胸径模型[6, 20-21],这些模型不仅能够模拟树高-胸径间的关系,而且在生物学上具有可解释性(表2)。采用R 4.00软件进行数据处理和传统模型拟合。
表 2 广义树高-胸径模型表达式
Table 2. Expression of referenced generalized height-diameter models
模型编号 Model No. 模型表达式 Model form 模型来源 References M1 $H = 1.3 + a0 \times {H_t}^{a1} \times {{\rm e}^{ - \frac{{a2}}{D}}}$ 王明亮,唐守正[22] M2 $H = 1.3 + \dfrac{{\left( {a0 + a1 \times {H_t}} \right) \times D}}{{a2 + D}}$ 胥辉[23] M3 $H{\rm{ = }}1.3 + \left( {a0 + a1 \times {H_t} - a2 \times {D_g}} \right) \times {{\rm e}^{ - \frac{{a3}}{{\sqrt D }}}}$ Schroder and Alvarez-Gonzalez[6] M4 $H{\rm{ = }}1.3{\rm{ + }}a0 \times {H_t}^{a1} \times {(1 - {{\rm e}^{ - a2 \times {D_g}^{ - a3} \times D}})^{a4}}$ Sharma and Parlon[24] M5 $H{\rm{ = }}1.3{\rm{ + }}\left( {{H_t} - 1.3} \right) \times \dfrac{{1 - {{\rm e}^{ - a0 \times D}}}}{{1 - {{\rm e}^{ - a0 \times {D_t}}}}}$ Meyermodefied[25] M6 $H{\rm{ = }}1.3{\rm{ + }}{\left( {a0 \times \left( {\dfrac{1}{D} - \dfrac{1}{{{D_g}}}} \right) + {{\left( {\dfrac{1}{{1.3 \times {H_t}}}} \right)}^{\dfrac{1}{2}}}} \right)^{ - 2}}$ Loetsch[6] M7 $H{\rm{ = }}1.3{\rm{ + }}\left( {{H_t} - 1.3} \right) \times {\left( {1 + a0 \times \left( {{H_t} - 1.3} \right) \times \left( {\dfrac{1}{D} - \dfrac{1}{{{D_t}}}} \right)} \right)^{ - 1}}$ Tome [26] M8 $H{\rm{ = }}1.3{\rm{ + }}a0 \times {H_t}^{a1} \times {D^{a2 \times {H_t}^{a3}}}$ Hui and KV[26] M9 $H = {H_t} \times \left( {1{\rm{ + }}\left( {a0 \times {H_t} \times a1 + a2 \times {D_g}} \right) \times {{\rm e}^{a3 \times {H_t}}}} \right) \times \left( {1 - {{\rm e}^{\frac{{a4 \times D}}{{{H_t}}}}}} \right)$ Soares and Tome [27] M10 $H = {\left( {{{1.3}^{a0}} + \left( {{H_t}^{a0} - {{1.3}^{a0}}} \right) \times \dfrac{{1 - {{\rm{e}}^{ - a1 \times D}}}}{{1 - {{\rm{e}}^{ - a1 \times {D_t}}}}}} \right)^{\frac{1}{{a0}}}}$ Castedo Dorado et [28] 注:表中H、D、Dt、Ht和Dg分别为树高(m)、胸径(cm)、优势胸径(cm)、优势高(m)和平均胸径(cm)。ai(i=0,1,2,3,4)为模型参数。
In the table, H, D, Dt,Ht and Dg are tree height (m), diameter at breast height (cm), dominant diameter at breast height (cm) dominant height (m) and average diameter at breast height (cm), respectively. ai(i=0,1,2,3,4)are parameters of models -
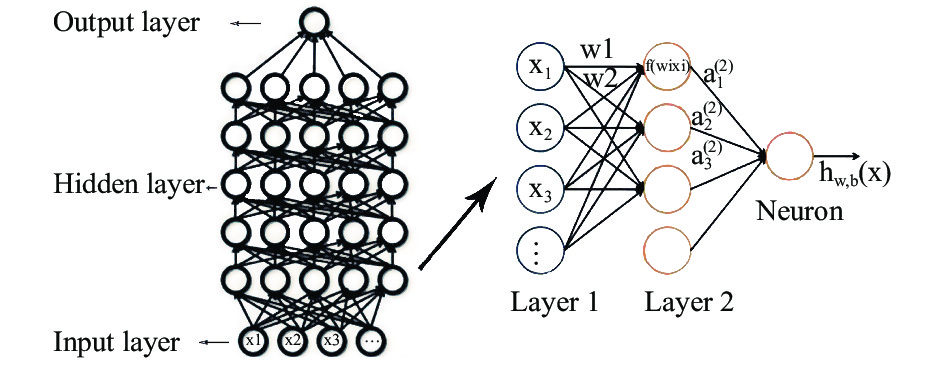
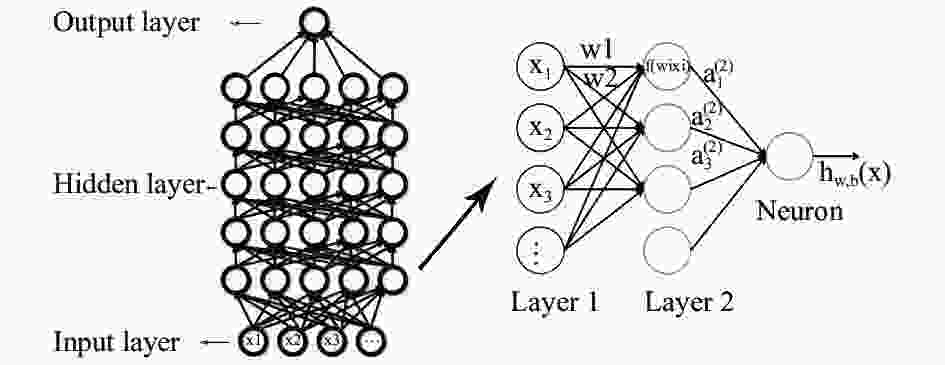
深度学习通常的模型结构为输入层、多层隐藏层与输出层,包含多层隐藏层和更多的神经元个数,能够拟合更复杂模型和处理更高维特征的数据。自输入层开始,一层一层地前馈训练,隐藏层的权重为双向的,分别是向上的“认知”权重和向下的“生成”权重,通过一定的方法(例如通过正则化对权重进行惩罚)使误差逐层传输,并不断对网络结构进行调整,最大限度地让认知和生成达成一致。每一个神经元都是一个激活函数,彼此通过权重连接。其大致的学习过程如图1表示,在图中,每个节点表示一个计算过程及结果,父节点计算的结果通过权重链接传递给子节点处,再次进行计算……直到寻找到成本函数的最小值。
-
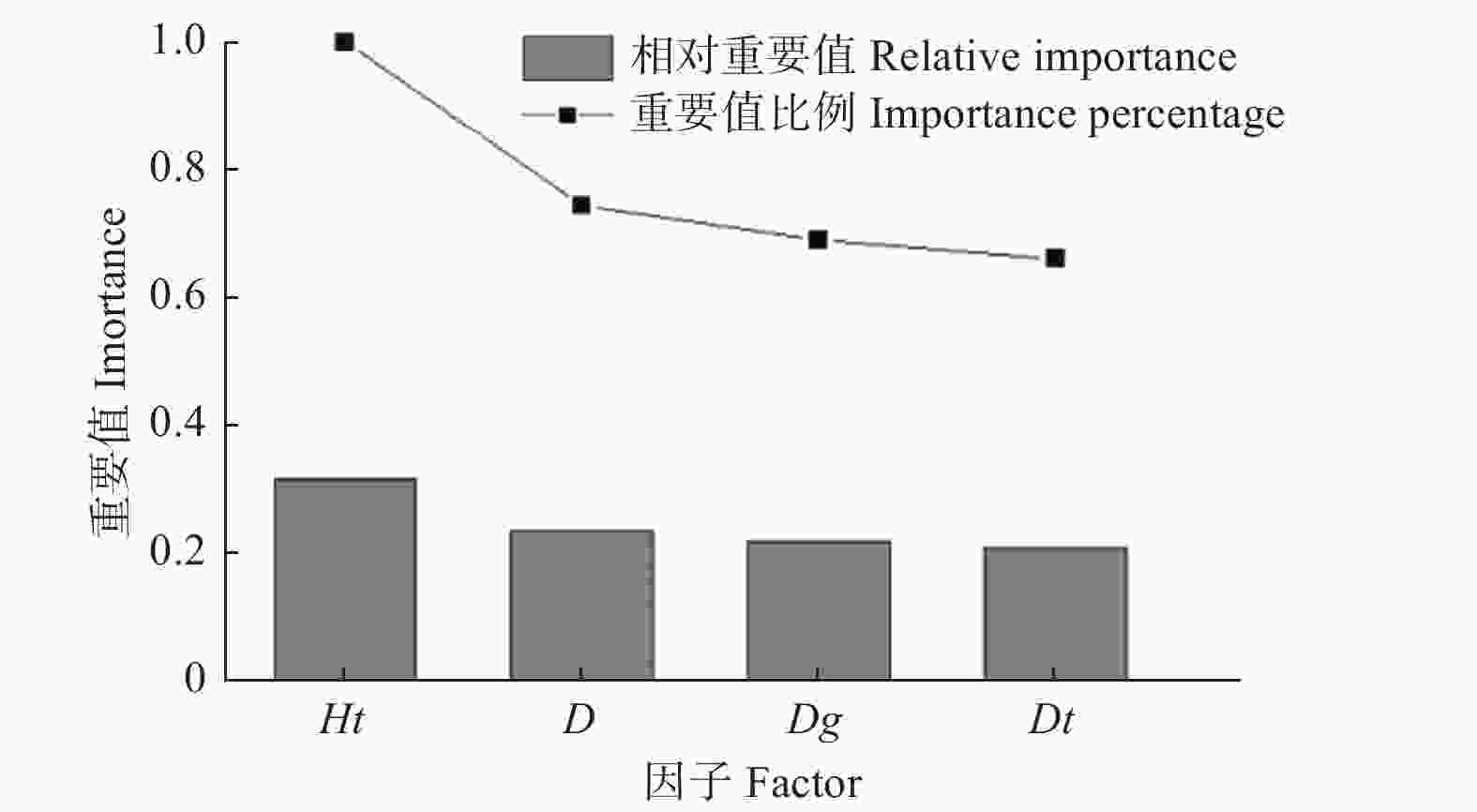
研究基于H2O平台构建DLA模型,H2O是一个开源、可扩展的分析预测平台,用于建立大数据模型,实现高精度预测。采用Python(Python 3.8)软件的h2o.estimators.deeplearning模块构建多层前馈神经网络模型。根据各变量的重要值排序结果(图2)可以看出,优势胸径的重要值很小,所以不考虑该变量。模型的输入变量为胸径、优势树高和林分平均胸径,输出变量为树高。此外,DLA模型同其他AI模型一样,需要确定隐藏层数量、激活函数类型和神经元个数等参数。通过前期比较分析,发现“Rectifier”作为传递函数的拟合结果优于其他函数,所以选择“RectifierWithDropout”作为DLA模型的激活函数。选择均方根误差(RMSE)作为梯度下降目标,H2O在训练DLA模型过程中采用自学习率算法,所以为了避免过拟合,将迭代次数设置为1 000,训练误差为0.001。
隐藏层数量和神经元个数是训练模型最基本的参数,决定了模型结构。本研究参考Ercanl的研究方法[29],为了确定神经元个数范围,首先将神经元个数从100~500,步长设置为50,发现在200~400之间,模型的结果表现较好,且各项指标较稳定。然后将每个隐藏层的神经元个数设置为200~400之间,间隔为20,同时采用H2OGridSearch包中的随机搜索(“RandomDiscrete”)方法以提高收敛速度,当模型结果的范围缩小时,则结合H2OGridSearch包中网格搜索的方式确定最优模型结构。同时为了减少误差提高精度,采用K折交叉验证训练DLA模型(nfold=5)。
通过深度学习,计算出输入因子的重要值和相对重要值比例,根据结果绘制图2,可以直观地看出各输入因子的对树高的重要程度。
-
采用调整后决定系数(R2),均方根误差(RMSE),平均绝对误差(MAE)和均方差(MSE)对模型的拟合精度和预测精度进行评价。R2越接近1,其余指标越接近0,模型的精度越高。结合残差图和拟合图评价,预测值越接近观测值,残差范围越小,分布越集中在Y=0两侧,模型越好。
-
传统模型的拟合统计结果如表3,包括各模型的参数估计值、调整后决定系数(R2)、均方根误差(RMSE)和平均误差(MAE)。可以看出,参数的估计结果大多具有可靠性(p < 0.001),这10个备选的基础模型的R2都在0.7以上,能够反映树高-胸径间的关系。不同模型对杉木胸径-树高关系的拟合精度不同,精度较低的3个模型分别是M5、M7和M10,其R2约为0.72,剩余模型的R2均在0.80以上。M6模型的精度明显高于其他模型,是对杉木树高-胸径关系拟合效果最好的模型,其R2最大,为0.84,RMSE和MAE分别是2.142和1.678,小于其他模型。所以选择M6作为DLA模型的对照。
表 3 模型参数估计及统计检验
Table 3. Parameter estimations and goodness-of-fit statistics of models
模型
Model参数 评价指标 a0 a1 a2 a3 a4 R2 RMSE MAE M1 5.799 4*** 0.502 7*** 10.870 6*** — — 0.80 2.449 1.901 0.438 9 0.022 3 0.180 7 — — M2 21.741 5*** 1.000 9*** 36.640 9*** — — 0.81 2.433 1.908 1.460 1 0.039 2 1.772 4 — — M3 24.938 5*** 0.990 2*** −0.287 6 5.390 1*** — 0.81 2.413 1.873 1.573 3 0.064 9 0.057 8 0.096 6 — M4 6.495 0*** 0.432 9*** 0.046 2*** −0.078 2* 1.186 4*** 0.81 2.398 1.864 0.645 4 0.029 4 0.006 1 0.035 2 0.060 1 M5 0.019 6*** — — — — 0.73 2.887 2.164 0.000 9 — — — — M6 −0.258 4*** — — — — 0.84 2.142 1.678 0.008 2 — — — — M7 0.947 1*** — — — — 0.72 2.891 2.146 0.012 8 — — — — M8 0.263 8* 0.655 8*** 0.896 5*** −0.089 7 — 0.80 2.468 1.952 0.126 4 0.151 6 0.228 6 0.080 2 — M9 −2.973 3*** 0.182 7*** 0.058 3* −0.115 2*** −1.236 5*** 0.82 2.336 1.828 0.735 9 0.043 5 0.024 1 0.010 2 0.039 4 M10 0.644 7*** 0.045 3*** — — — 0.72 2.862 2.145 0.051 5 0.004 1 — — — 注:***表示p < 0.001,**表示0.001 < p < 0.01,*表示0.01 < p < 0.05,斜体是各参数的标准误
*** means p < 0.001, ** means 0.001 < p < 0.01, * means 0.01 < p < 0.05, italics are the standard errors of each parameter从70个DLA模型中,根据隐藏层的不同数量,选择拟合精度最优(R2最大,而RMSE、MAE、MSE最小)的模型列于表4。可以看出,表中所有DLA模型的R2均在0.85及以上,大于最优的传统模型,RMSE和MAE分别在2.1和1.6左右,均小于传统模型。说明DLA模型的拟合结果优于广义胸径-树高模型。其中,隐藏层数量为3和6,神经元个数分别为300和340的DLA模型精度高于其他结构,R2能达到0.85,RMSE和MAE也较其他模型更小。如果只考虑模型的精度,那么最优模型的结构为6个隐藏层,每个隐藏层有340个神经元。如果同时考虑建模效率,即考虑模型的收敛时间,那么最优模型的结构为3个隐藏层,每个隐藏层有300个神经元。
表 4 不同隐藏层的最优DLA模型统计
Table 4. Performance of best DLA models with different hidden layers
隐藏层数量
Hidden layers神经元个数
Neurons模型评价指标 收敛时间
Total interations/
minR2 MSE RMSE MAE 2 320 0.84 5.001 2.236 1.707 4 3 300 0.85 4.642 2.139 1.572 6 4 360 0.84 4.645 2.290 1.566 7 5 340 0.84 4.929 2.241 1.613 10 6 340 0.85 4.245 2.105 1.457 13 7 340 0.84 5.024 2.333 1.648 16 8 340 0.84 5.208 2.492 1.663 20 DLA模型也是类似“黑箱”结构,缺乏可解释性。为了进一步分析DLA模型,比较传统模型和DLA模型的拟合精度,绘制图3,该图展示了观测值和预测值的分布关系,也展示了优势高、胸径对单木树高的影响。可以看出,预测值均匀分布在真实值之间,说明模型能较准确地模拟杉木的树高、胸径和优势高之间的关系。当胸径一定时,树高随着林分优势高的增加而增加,当优势高一定时,树高随着胸径的增加而增加,说明DLA模型符合树高生长的生物学规律。比较两个模型的拟合结果,可以看出,对于较高的林木,DLA模型比传统模型的拟合效果更好。
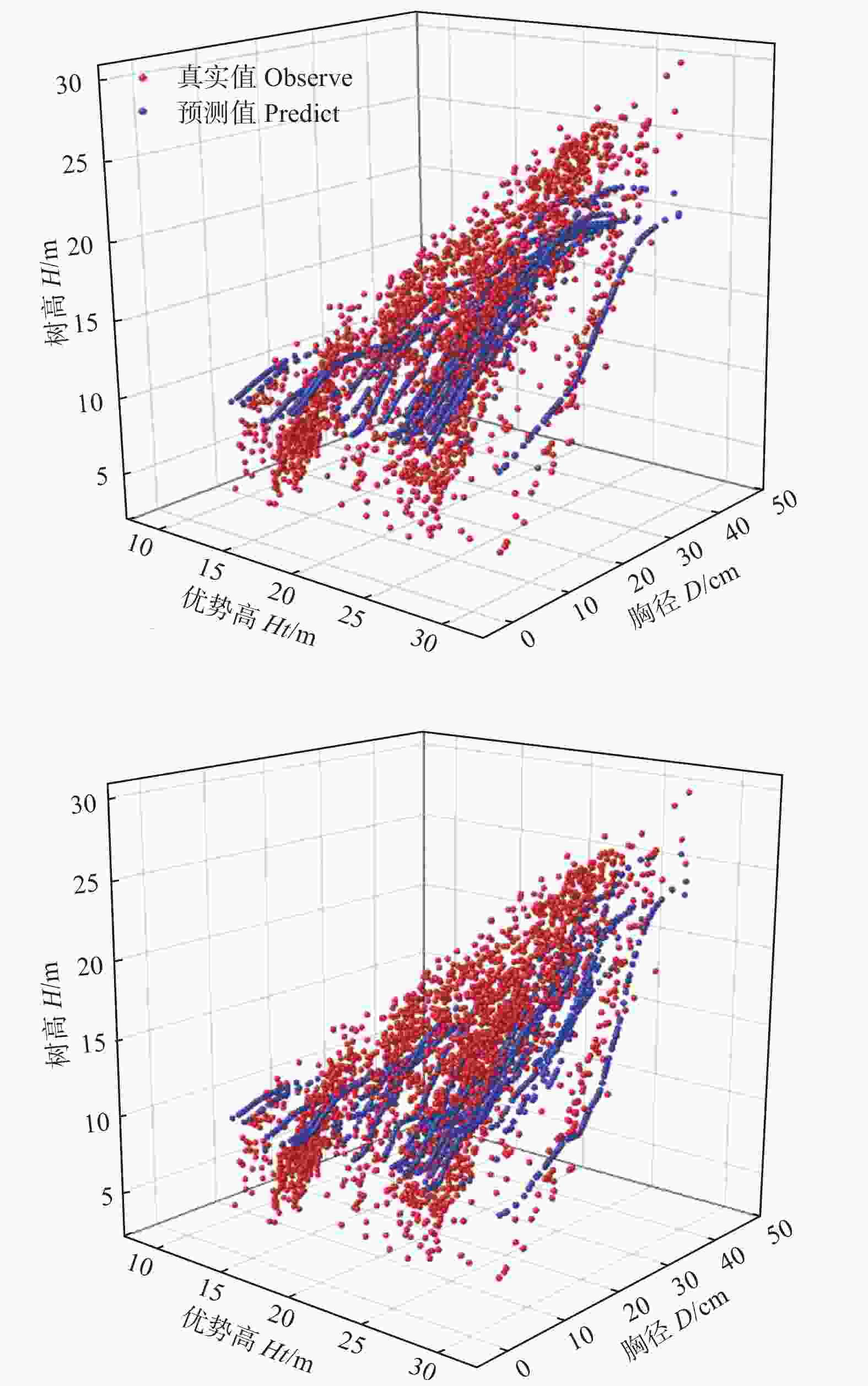
图 3 最优传统模型与最优DLA模型的拟合结果比较
Figure 3. Comparition fitting results of best traditional model and best DLA model
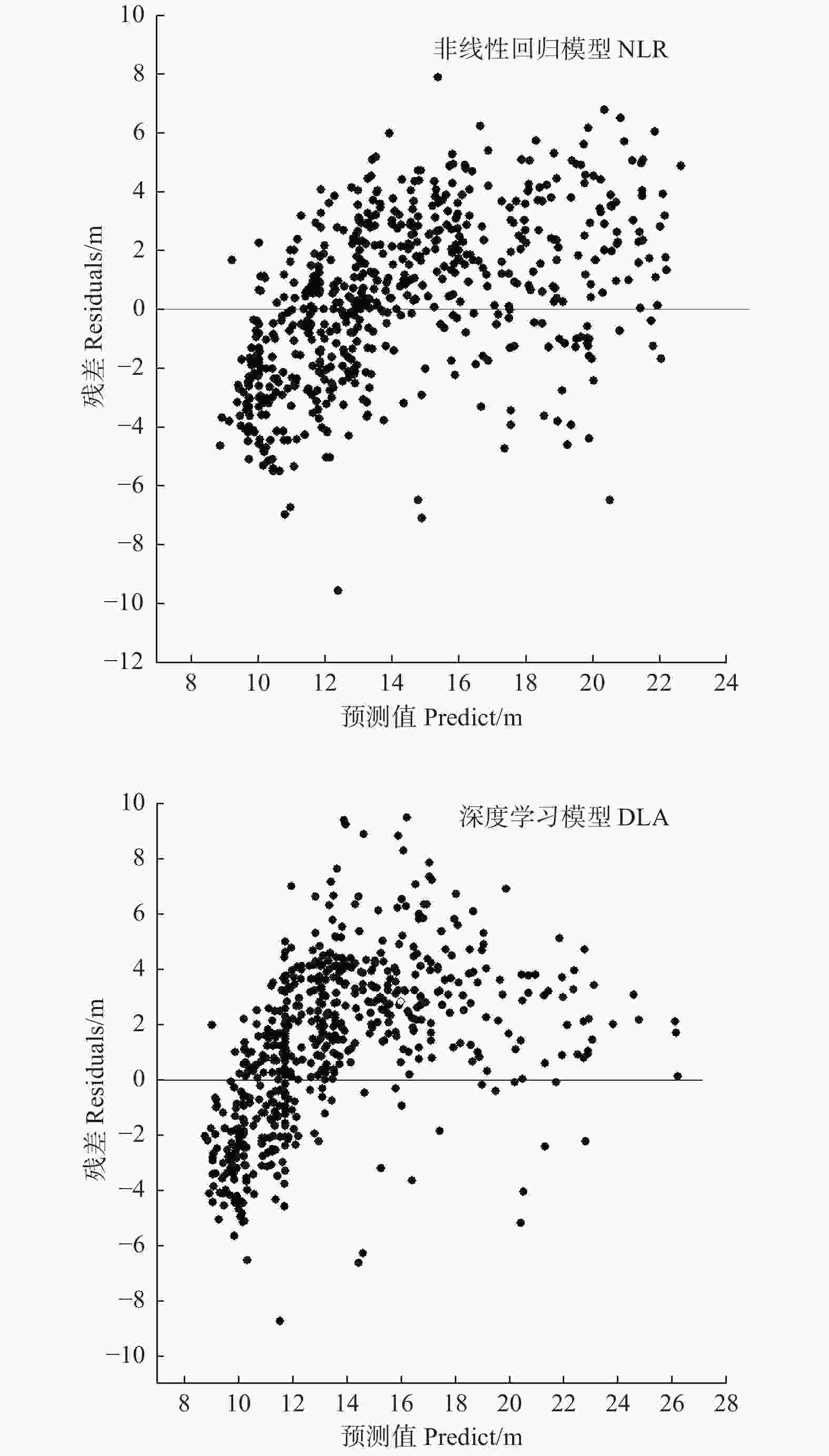
分别选取最优的传统回归模型和DLA模型,采用未建模的数据进行独立性检验,以确定DLA模型是否存在过拟合问题,同时比较两种模型对杉木树高的预测能力。由表5可以看出,DLA模型独立性检验的R2为0.838,与训练集相差很小,RMSE和MAE值也与训练集相当,说明DLA模型不存在过拟合的问题。而且,可以看出DLA模型的预测精度高于传统模型,R2大于传统模型,RMSE和MAE也分别减小了9.62%和14.64%。图4描述了两种模型预测值和对应残差的分布关系,由残差图可以看出,DLA模型的残差更为集中,尤其在树高H > 18 m时,残差大多在−3~5 m的范围内,小于传统回归。说明DLA模型预测精度高于传统回归模型,并且当预测较高的林木时,这种优势愈明显。
表 5 模型检验结果
Table 5. Validation of models
模型
Models决定系数
R2均方根误差
RMSE/m平均绝对误差
MAE/mDLA模型 0.838 2.197 1.669 M6模型 0.835 2.267 1.841 -
本研究基于H20数据分析平台的深度学习算法,采用Python软件构建杉木的胸径-树高DLA模型,这些平台与软件均是开源免费,容易获得,成本低、实用性强。与传统的建模方法相比,深度学习对数据分布结构没有要求,建模前不需要确定模型的具体形式,而且更易收敛,能最大限度地逼近现实关系[30]。Ercanli等人构建了80个DLA模型结构预测杜克松的树高,隐藏层数为3~10,每层神经元个数是10~100,步长为10,发现每层100个神经元的结构精度最高[29]。考虑到本研究的样本量更大,神经元个数从100开始,同时为了防止过拟合,神经元个数不能太大。还发现当隐藏层为3~8时,随着神经元个数的增加,模型的整体表现有所提升。而7、9、10层的DLA模型表现不如层数更少的,认为是由于层数太多,结构过复杂而使相关参数值不能满足。所以本研究的隐藏层数量设置为2~8层,在建立DLA模型过程中也发现,随着隐藏层数的增加,收敛速度变得越来越慢,且精度并没有明显提升,说明复杂的结构不一定能使模型表现更好,应该根据输入变量结构选择合适的隐藏层数。
结果表明,不同结构的DLA模型均能较好地描述树高与胸径间的关系。无论在建模数据集还是检验数据集上,DLA模型的R2均大于广义树高-胸径模型,RMSE和MAE均小于广义树高-胸径模型,说明DLA模型的精度高于传统回归模型,与前人的研究结论一致。Ercanli等人基于深度学习对土耳其西北部地区的杜克松建立了树高-胸径DLA模型[30],Shen等人采用以广东地区的毛白杨为对象,建立包含多隐藏层的树高-胸径BP-ANN模型[15],都表明多隐藏层模型能更逼近胸径-树高的真实关系。尽管研究的树种和地区都不相同,但都有类似结果,这说明多隐藏层的神经网络模型,也可能适用于其他地区、其他树种的树高预测。在训练DLA模型时,与人工神经网络模型一样,需要注意过拟合问题,本研究得到精度最高的DLA模型包含6个隐藏层,每个隐藏层有340个神经元,如果同时考虑模型的收敛速度,则最优的模型结构为3个隐藏层,每个隐藏层各有300个神经元,其独立性检验结果与训练结果相差不大,说明没有出现过拟合。该模型还可以用于预测其他单木参数(冠幅、材积、生长量)或林分特征(断面积、蓄积、碳储量)。
本研究证明深度学习算法预测杉木树高的适用性,能够作为传统回归的补充,尽管目前深度学习模型还存在可解释差、技术门槛高,但随着计算机技术和人工智能的飞速发展,相信这些问题很快能得到解决,深度学习在林业领域的应用前景值得期待。当模型只需考虑精度,或数据分布不满足统计学假设时,可以采用深度学习算法,代替传统统计学方法。但是深度学习与其他人工智能算法一样,存在“黑箱”问题,由于不能明确表达内部结构,所以缺少可解释性[17],这也是由于对这一技术的不熟悉,应该投入研究挖掘建模的原理,以便被更广泛地理解和应用。本次研究中,只有胸径、林分优势高、林分优势胸径和林分平均高4个输入变量,而树高生长还会受到更多因素的影响,如气象因子(年均温、年降水量)和其他林分因子(年龄、密度、大树断面积),未来的模型中可以加入这些因子,也许能进一步提高模型精度。尽管在本研究中,建立的DLA模型精度高于传统回归模型,但还没有比较其他的模型形式,也未与混合效应方法进行比较,而且深度学习预测树高仍然是一个较新的方法,少有其他的研究结论,所以其精度是否均高于传统模型还不能确定,需要更深入的探究,在未来的研究中,可以探究更多的树高-胸径模型形式,或比较其他的传统建模方法。此外,基于大数据的多变量或相当复杂的非线性问题上,深度学习技术的优势更加突出,所以当对大尺度的森林资源进行监测时,该方法可能更为适用。
-
本研究采用福建省将乐国有林场的34块杉木标准地调查数据,基于H2O平台的深度学习算法,建立了多个杉木树高-胸径的DLA模型。同时采用传统非线性回归建立10个广义树高-胸径模型用以比较。研究结果表明:(1)不同隐藏层数量的DLA模型均能较好地描述杉木的树高-胸径间关系,其R2约为0.84~0.85,大于最优传统模型的0.84,RMSE和MAE也更小。而且,DLA模型的预测泛化能力也高于传统模型。在采用相同建模数据的情况下,DLA模型可以提高杉木树高预测的精度,且当预测较高的杉木时,这种优势更为明显。(2)精度最高的DLA模型,其模型结构为6个隐藏层,每个隐藏层各有340个神经元,可用于研究区杉木树高的估测。(3)与传统建模方法相比,深度学习不受统计学假设的限制,建模前不需要确定模型具体形式,更容易收敛。在预测森林参数、构建森林模型方面具有可行性,某些情况下能够作为传统模型的替代方法。
深度学习和传统方法模拟杉木树高-胸径模型比较
Comparison of Deep Learning and Traditional Models to Simulate the Height-DBH Relationship of Chinese Fir
-
摘要:
目的 基于深度学习算法,建立多隐藏层的杉木树高-胸径神经网络模型,探索一种更高效低偏的树高模型研建方法,提高杉木树高的预测精度。 方法 利用福建省将乐国有林场34块杉木样地的2898组树高-胸径调查数据,基于传统回归建立10个广义树高-胸径模型,筛选出精度最高的模型作为对照。同时基于H2O平台的深度学习算法,建立70个不同结构的树高-胸径DLA模型,通过分析比较,确定最适宜预测杉木树高的模型结构,与传统最优模型进行比较。 结果 建立的树高-胸径DLA模型均能较好地描述杉木的树高-胸径间关系,R2都在0.84以上,大于最优传统模型,RMSE和MAE小于传统模型。精度最高的DLA模型结构包含6个隐藏层,每层各340个神经元。 结论 本研究基于深度学习建立的杉木树高-胸径DLA模型,其拟合精度与预测精度略高于传统的广义树高-胸径模型,尤其在预测较高的林木时,更为明显,能够用于研究区杉木树高的预测。 Abstract:Objective To explore a more efficient and low-biased tree height prediction method, improve the prediction accuracy of tree height, and to establish a multi-hidden layer neural network model of height- diameter is based on deep learning algorithm. Method Using a set of 2898 groups of tree height and diameter data from 34 Chinese Fir (Cunninghamia lanceolata) sample plots in Jiangle National Forest Farm of Fujian Province, 10 generalized height-diameter models were established based on traditional regression, and the model with the highest accuracy was selected to compare. At the same time, based on the deep learning algorithm of the H2O platform, 70 DLA models with different structures of tree height-diameter at breast height were established. Through analysis and comparison, the most suitable model structure was determined and compared with the traditional optimal model. Result The different height-diameter DLA models can describe the relationship between height and diameter of Chinese Fir well, whose R2 is above 0.84, which is higher than that of the best traditional model, and the RMSE and MAE are smaller than that of the traditional model. The most accurate DLA model structure contains 6 hidden layers, each with 340 neurons. Conclusion The height-diameter DLA model established based on deep learning has higher fitting accuracy and prediction accuracy than the traditional models, especially when predicting higher trees. It can be used to predict the height of Chinese Fir in study area. -
Key words:
- deep learning
- / height-diameter model
- / nonlinear regression
- / Chinese Fir
-
表 1 建模数据和见证数据统计
Table 1. Summary statistics of modeling set and validation set
测树因子
Statistics建模数据 Train set 检验数据 Validation set 最小值 Min 最大值 Max 平均值 Mean 标准差 sd 最小值 Min 最大值 Max 平均值 Mean 标准差 sd 胸径 D/cm 3.9 43.5 16.4 7.18 4.4 44.5 16.6 7.59 树高 H/m 2.9 30.5 14.5 5.46 4.5 27.8 14.9 6.14 优势胸径 Dt/cm 14.9 39.9 26.6 6.24 14.9 39.9 26.6 5.73 优势树高 Ht/m 11.3 30.5 22.1 4.80 11.3 30.5 22.3 4.69 平均胸径 Dg/cm 9.9 28.1 17.2 4.91 9.9 28.1 17.4 5.04 表 2 广义树高-胸径模型表达式
Table 2. Expression of referenced generalized height-diameter models
模型编号 Model No. 模型表达式 Model form 模型来源 References M1 $H = 1.3 + a0 \times {H_t}^{a1} \times {{\rm e}^{ - \frac{{a2}}{D}}}$ 王明亮,唐守正[22] M2 $H = 1.3 + \dfrac{{\left( {a0 + a1 \times {H_t}} \right) \times D}}{{a2 + D}}$ 胥辉[23] M3 $H{\rm{ = }}1.3 + \left( {a0 + a1 \times {H_t} - a2 \times {D_g}} \right) \times {{\rm e}^{ - \frac{{a3}}{{\sqrt D }}}}$ Schroder and Alvarez-Gonzalez[6] M4 $H{\rm{ = }}1.3{\rm{ + }}a0 \times {H_t}^{a1} \times {(1 - {{\rm e}^{ - a2 \times {D_g}^{ - a3} \times D}})^{a4}}$ Sharma and Parlon[24] M5 $H{\rm{ = }}1.3{\rm{ + }}\left( {{H_t} - 1.3} \right) \times \dfrac{{1 - {{\rm e}^{ - a0 \times D}}}}{{1 - {{\rm e}^{ - a0 \times {D_t}}}}}$ Meyermodefied[25] M6 $H{\rm{ = }}1.3{\rm{ + }}{\left( {a0 \times \left( {\dfrac{1}{D} - \dfrac{1}{{{D_g}}}} \right) + {{\left( {\dfrac{1}{{1.3 \times {H_t}}}} \right)}^{\dfrac{1}{2}}}} \right)^{ - 2}}$ Loetsch[6] M7 $H{\rm{ = }}1.3{\rm{ + }}\left( {{H_t} - 1.3} \right) \times {\left( {1 + a0 \times \left( {{H_t} - 1.3} \right) \times \left( {\dfrac{1}{D} - \dfrac{1}{{{D_t}}}} \right)} \right)^{ - 1}}$ Tome [26] M8 $H{\rm{ = }}1.3{\rm{ + }}a0 \times {H_t}^{a1} \times {D^{a2 \times {H_t}^{a3}}}$ Hui and KV[26] M9 $H = {H_t} \times \left( {1{\rm{ + }}\left( {a0 \times {H_t} \times a1 + a2 \times {D_g}} \right) \times {{\rm e}^{a3 \times {H_t}}}} \right) \times \left( {1 - {{\rm e}^{\frac{{a4 \times D}}{{{H_t}}}}}} \right)$ Soares and Tome [27] M10 $H = {\left( {{{1.3}^{a0}} + \left( {{H_t}^{a0} - {{1.3}^{a0}}} \right) \times \dfrac{{1 - {{\rm{e}}^{ - a1 \times D}}}}{{1 - {{\rm{e}}^{ - a1 \times {D_t}}}}}} \right)^{\frac{1}{{a0}}}}$ Castedo Dorado et [28] 注:表中H、D、Dt、Ht和Dg分别为树高(m)、胸径(cm)、优势胸径(cm)、优势高(m)和平均胸径(cm)。ai(i=0,1,2,3,4)为模型参数。
In the table, H, D, Dt,Ht and Dg are tree height (m), diameter at breast height (cm), dominant diameter at breast height (cm) dominant height (m) and average diameter at breast height (cm), respectively. ai(i=0,1,2,3,4)are parameters of models表 3 模型参数估计及统计检验
Table 3. Parameter estimations and goodness-of-fit statistics of models
模型
Model参数 评价指标 a0 a1 a2 a3 a4 R2 RMSE MAE M1 5.799 4*** 0.502 7*** 10.870 6*** — — 0.80 2.449 1.901 0.438 9 0.022 3 0.180 7 — — M2 21.741 5*** 1.000 9*** 36.640 9*** — — 0.81 2.433 1.908 1.460 1 0.039 2 1.772 4 — — M3 24.938 5*** 0.990 2*** −0.287 6 5.390 1*** — 0.81 2.413 1.873 1.573 3 0.064 9 0.057 8 0.096 6 — M4 6.495 0*** 0.432 9*** 0.046 2*** −0.078 2* 1.186 4*** 0.81 2.398 1.864 0.645 4 0.029 4 0.006 1 0.035 2 0.060 1 M5 0.019 6*** — — — — 0.73 2.887 2.164 0.000 9 — — — — M6 −0.258 4*** — — — — 0.84 2.142 1.678 0.008 2 — — — — M7 0.947 1*** — — — — 0.72 2.891 2.146 0.012 8 — — — — M8 0.263 8* 0.655 8*** 0.896 5*** −0.089 7 — 0.80 2.468 1.952 0.126 4 0.151 6 0.228 6 0.080 2 — M9 −2.973 3*** 0.182 7*** 0.058 3* −0.115 2*** −1.236 5*** 0.82 2.336 1.828 0.735 9 0.043 5 0.024 1 0.010 2 0.039 4 M10 0.644 7*** 0.045 3*** — — — 0.72 2.862 2.145 0.051 5 0.004 1 — — — 注:***表示p < 0.001,**表示0.001 < p < 0.01,*表示0.01 < p < 0.05,斜体是各参数的标准误
*** means p < 0.001, ** means 0.001 < p < 0.01, * means 0.01 < p < 0.05, italics are the standard errors of each parameter表 4 不同隐藏层的最优DLA模型统计
Table 4. Performance of best DLA models with different hidden layers
隐藏层数量
Hidden layers神经元个数
Neurons模型评价指标 收敛时间
Total interations/
minR2 MSE RMSE MAE 2 320 0.84 5.001 2.236 1.707 4 3 300 0.85 4.642 2.139 1.572 6 4 360 0.84 4.645 2.290 1.566 7 5 340 0.84 4.929 2.241 1.613 10 6 340 0.85 4.245 2.105 1.457 13 7 340 0.84 5.024 2.333 1.648 16 8 340 0.84 5.208 2.492 1.663 20 表 5 模型检验结果
Table 5. Validation of models
模型
Models决定系数
R2均方根误差
RMSE/m平均绝对误差
MAE/mDLA模型 0.838 2.197 1.669 M6模型 0.835 2.267 1.841 -
[1] 曾 翀, 雷相东, 刘宪钊, 等. 落叶松云冷杉林单木树高曲线的研究[J]. 林业科学研究, 2009, 22(2):182-189. doi: 10.3321/j.issn:1001-1498.2009.02.006 [2] Castaño-Santamaría J, Crecente-Campo F, Fernández-Martínez J L, et al. Tree height prediction approaches for uneven-aged beech forests in northwestern Spain[J]. Forest Ecology and Management, 2013, 307: 63-73. doi: 10.1016/j.foreco.2013.07.014 [3] 张 鹏, 何怀江, 范春雨, 等. 吉林蛟河针阔混交林主要树种树高-胸径模型[J]. 林业科学研究, 2018, 31(2):11-18. [4] Diamantopoulou M J, özçelik R. Evaluation of different modeling approaches for total tree-height estimation in Mediterranean Region of Turkey[J]. Forest Systems, 2012, 21(3): 383-397. doi: 10.5424/fs/2012213-02338 [5] 庄崇洋, 黄清麟, 马志波, 等. 典型中亚热带天然阔叶林各林层树高胸径关系研究[J]. 林业科学研究, 2017, 30(3):479-485. [6] Mehtätalo L, De-Miguel S, Gregoire T G. Modeling height-diameter curves for prediction[J]. Canadian Journal of Forest Research, 2015, 45(7): 826-837. doi: 10.1139/cjfr-2015-0054 [7] 刘 鑫, 王海燕, 雷相东, 等. 基于BP神经网络的天然云冷杉针阔混交林标准树高-胸径模型[J]. 林业科学研究, 2017, 30(3):368-375. [8] 卯光宪, 谭 伟, 柴宗政, 等. 基于BP神经网络的马尾松人工林胸径-树高模型预测[J]. 浙江农林大学学报, 2020, 37(4):752-760. [9] 樊 伟, 许崇华, 崔 珺, 等. 基于混合效应的大别山地区杉木树高-胸径模型比较[J]. 应用生态学报, 2017, 28(9):2831-2839. [10] 刘兆华, 林 辉, 龙江平, 等. 基于高分二号的旺业甸林场蓄积量估测模型研究[J]. 中南林业科技大学学报, 2020, 40(3):79-84. [11] 李春明, 李利学. 基于非线性混合模型的栓皮栎树高与胸径关系研究[J]. 北京林业大学学报, 2009, 31(4):7-12. doi: 10.3321/j.issn:1000-1522.2009.04.002 [12] Nunes M H, Gorgens E B. Artificial intelligence procedures for tree taper estimation within a complex vegetation mosaic in Brazil[J]. PLOS ONE, 2016, 11(5): 1371-1384. [13] Tavares Júnior I, Rocha J, Ebling Â, et al. Artificial neural networks and linear regression reduce sample intensity to predict the commercial volume of Eucalyptus clones[J]. Forests, 2019, 10(3): 268. doi: 10.3390/f10030268 [14] özçelık R, Diamantopoulou M J, Eker M, et al. Artificial neural network models: An alternative approach for reliable aboveground pine tree biomass prediction[J]. Forest Science, 2017, 63(3): 291-302. doi: 10.5849/FS-16-006 [15] Shen J, Hu Z, Sharma R P, et al. Modeling height–diameter relationship for poplar plantations using combined-optimization multiple hidden layer back propagation neural network[J]. Forests, 2020, 11(4): 442. doi: 10.3390/f11040442 [16] Ercanli İ. An application of R software model based on deep learning algorithms to provide future use of other forest practitioner for predicting individual tree height[J]. Anatolian Journal of Forest Research, 2019, 2(5): 110-119. [17] 雷向东. 机器学习算法在森林生长收获预估中的应用[J]. 北京林业大学学报, 2019, 42(12):23-36. doi: 10.12171/j.1000-1522.20190356 [18] 孙立研, 刘美玲, 周礼祥, 等. 基于气象因子深度学习的森林火灾预测方法[J]. 林业工程学报, 2019, 4(3):132-136. [19] Pleșoianu A, Stupariu M, Sandric I, et al. Individual tree-crown detection and species classification in very high-resolution remote sensing imagery using a deep learning ensemble model[J]. Remote Sensing, 2020, 12(15): 2426. doi: 10.3390/rs12152426 [20] 董云飞, 孙玉军, 许 昊. 3种标准树高曲线建立方法的比较[J]. 西北农林科技大学学报: 自然科学版, 2015, 43(11):82-90. [21] Sharma M, Parton J. Height–diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach[J]. Forest Ecology & Management, 2007, 249(3): 187-198. [22] 王明亮, 唐守正. 标准树高曲线的研制[J]. 林业科学研究, 1997, 10(3):36-41. [23] 胥 辉, 全宏波, 王 斌. 思茅松标准树高曲线的研究[J]. 西南林学院学报, 2000, 20(2):74-77. [24] Sharma M., Smith M., Burkhart H. E., et al. Modeling the impact of thinning on height development of dominant and codominant loblolly pine trees[J]. Annals of Forest Science, 2006, 63(4): 349-354. [25] Gadow K V, Hui G. Modelling forest development[J]. Forestry Sciences, 1999, 57(12): 1146-1158. [26] Lynch T B, Gordon H A, Stevenson D J. A random-parameter height-dbh model for cherrybark oak[J]. Southern Journal of Applied Forestry, 2005(1): 22-26. [27] Soares P, Tomé M. Height–diameter equation for first rotation eucalypt plantations in Portugal[J]. Forest Ecology & Management, 2002, 166(1-3): 99-109. [28] Castedo D F, Barrio A M, Parresol B R, et al. A stochastic height-diameter model for maritime pine ecoregions in Galicia (northwestern Spain)[J]. Annals of Forest Science, 2005, 62(5): 455-465. doi: 10.1051/forest:2005042 [29] Ercanli I. Innovative deep learning artificial intelligence applications for predicting relationships between individual tree height and diameter at breast height[J]. Forest Ecosystems, 2020, 7(1): 7-12. doi: 10.1186/s40663-020-0216-9 [30] Ercanli I. Artificial intelligence with deep learning algorithms to model relationships between total tree height and diameter at breast height[J]. Forest Systems, 2020, 29(2): e103. -



 下载:
下载: