-
林分密度指标是评定一个时期林分生长密度的尺度指标,而确定合适的指标是开展林分密度研究的重要前提。Dean[1]认为林分密度指标则至少需要满足以下3个条件:(1)与林分生长有关;(2)与立地质量、林分年龄等无内在联系;(3)较为容易测量得到。林分密度指标有多种,如:Reineke林分密度指数(SDI)[2],Nilson密度指数 (SD)[3-4],优势高-营养面积比[5],相对密度RD指数[6],以及相对植距RS指数[7]等。这些密度指标的提出均是处于一定的条件下,每个指标都有其使用条件及适用范围。选用不同的林分密度指标会直接影响着所建模型的精度与预估结果,因此选取合适的密度指标建立单木生长模型显得尤为重要。
基于林木长期生长数据,预估单木年生长量时,之前常用的固定生长率法是假设在森林的整个生长期内,林木的生长率是固定不变的这一假设进行的研究。显而易见,这种假设并不符合现实规律,随着林分生长时间的推移,所用于预估模型中的特征因子(林分优势高、林龄、林分密度)和林分中单木的特征因素(树高、胸径)等在每一个生长阶段都会有变化,必然也会导致单木生长量的变化。为克服固定生长率法的这个缺陷,不少方法被陆续提出,如内插法和迭代法等。Cao等[8]基于迭代法提出的可变生长率法。该方法将林分生长期间林分与单木因子变化引起的单木年生长量变化纳入分析,并且用时比迭代法更少。张雄清等[9]比较了可变生长率法与固定生长率法,发现可变生长率法表现更好。
杉木(Cunninghamia lanceolata (Lamb.) Hook.)是中国南部地区最重要的用材林树种。本研究基于可变生长率法构建包含不同林分密度指标的杉木单木直径年生长模型,选出适宜单木直径年生长模型的最优林分密度指标,以期实现杉木人工林单木直径生长的精准预测,为实现杉木人工林质量精准提升提供密度管理支撑依据。
-
样地设置在福建武夷山北部的邵武市,位于117°43′ E, 27°05′ N。地貌特征主要是高山和低丘陵地区,海拔为250~700 m,坡度为25°~35°,为亚热带季风气候,年平均温度17.7 ℃,1月平均温度6.8 ℃,7月平均温度28 ℃,最低极端气温为−7.9 ℃,年日照时间1 740.7 h,平均霜冻期为95 d。年降水量1 768 mm,年平均相对湿度为82%。林下植被有中华杜英(Elaeocarpus chinensis (Gardn.et Champ.) Hook. F.ex Benth.)、胡颓子(Elaeagnus pungens Thunb.)、狗脊(Woodwardia japonica (L.f.) Sm.)、芒萁(Dicranopteris pedata (Houtt.) Nakaike)、乌毛蕨(Blechnum orientale L.)和扇叶铁线蕨(Adiantum flabellulatum L.)等。
试验林使用1年生苗木于1982年造林,完全随机区组设计,分5种造林密度:A:2 m × 3 m(1 667 株·hm−2),B:2 m × 1.5 m(3 333 株·hm−2),C:2 m × 1 m(5 000 株·hm−2),D:1 m × 1.5 m(6 667 株·hm−2)和E:1 m × 1 m(10 000 株·hm−2)。每个样地大小为20 m × 30 m,每种造林密度均重复3次,总计15个样地。标记了一共4 800棵树,在冬季测量树高和胸径,从1984年至1990年,每年进行1次测量;从1992年至2010年,每隔1或者2年进行1次测量。具体统计数据见表1。研究数据随机抽取60%用于模型构建,剩余40%用于模型验证。
表 1 杉木人工林林分和单木变量统计
Table 1. Summary statistics of stand and tree variables of Chinese fir plantation
变量
Variable最小值
Min.最大值
Max.平均值
Mean标准差
Standard deviation林龄 Age/a 4.0 28.0 14.3 7.6 株数 Number of trees/ (tree·hm−2) 1 175.0 10 000.0 4 617.3 2 557.4 优势高 Dominant height/m 2.9 26.9 12.7 6.1 单木胸径 Tree diameter/cm 3.6 39 9.3 5.1 断面积 Stand basal area/(m2·hm-2) 0.8 81.1 39.3 22.2 -
利用常用的7种林分密度指标,分别是每公顷株数密度N、每公顷胸高断面积Ba、林分密度SDI指数、SD指数、优势高—营养面积比Z指数、相对密度RD指数和相对植距RS指数构建杉木单木直径生长模型。
-
(1) SDI指数
SDI指数 [2]是通过单位面积上林木的株数与林木的平均胸径的关系确定的,是反映林分直径分布与林分内单位面积的株数之间关系的综合指标。因此,SDI密度指数在林木密度管理中使用较常见,其数学表达式为:
$ SDI={N\left(\frac{D\mathrm{q}}{D0}\right)}^{\beta } $
(1) 式中:Dq为林分平方平均胸径cm;D0—林分标准直径,杉木一般取值20 cm;β为Reinek自稀疏系数,一般取值−1.605。
(2) SD指数
根据Nilson[3-4]对林木之间的平均距离L和胸径Dq的定义,林分相对密度SD指数的公式如下[10]:
$ L=\frac{100}{{N}^{1/2}} $
$ D\mathrm{q}=a + bL $
$ SD=N{\left(\frac{D0 + k}{D\mathrm{q} + k}\right)}^{2} $
(2) 式中:a,b为参数,k=−a,D0—取20 cm。
(3)优势高—营养面积比Z指数
刘金福等[5]采用单位面积内株数与优势木的平均高来反映林分中林木的相对密度的大小。其表达式如下:
$ Z=\frac{N\times {H}_{\mathrm{d}}}{10\mathrm{ }000} $
(3) 式中:N—每公顷株数;Hd—优势木平均高。
(4) 相对密度RD指数
Curtis[6]提出利用林分断面积和平方平均胸径计算林分密度指标,该指标简单,容易计算[11],其公式如下:
$ RD=\frac{Ba}{\left({D\mathrm{q}}^{1/2}\right)} $
(4) (5)相对植距RS指数
相对植距是跟立地、胸径等因子无关的林分密度指标,表达式如下[7]:
$ RS=\frac{100}{{N}^{1/2}{H}_{\mathrm{d}}} $
(5) -
构建单木直径生长模型,可以引入多个自变量,其中包括单木特征因子(树高、胸径等)和林分特征因子(林分密度、林龄、林分优势高等)。一般这些因子归为3类:林龄、竞争因子和立地因子。而立地因子中,一般以林分优势高表示。因此,在单木的生长过程中,主要是受到竞争、立地和林龄的影响。在本研究中,选取了林龄(A)、7种林分密度指标和林分优势高(Hd)构建杉木单木直径生长模型。基于可变生长率法,利用递归的方式推导过程如下[9]:
(t + 1)年时:
$ {D}_{i,t + 1}={D}_{i,t} + \mathrm{exp}({\alpha }_{1} + {\alpha }_{2}\mathrm{*}{A}_{t} + {\alpha }_{3}\mathrm{*}K + \frac{{\alpha }_{4}}{\mathrm{log}\left({Hd}_{t}\right)} $
(6) (t + 2)年时:
$\begin{aligned} & {D}_{i,t + 2}={D}_{i,t + 1} + \mathrm{exp}({\alpha }_{1} + {\alpha }_{2}\mathrm{*}{A}_{t + 1} + {\alpha }_{3}\mathrm{*}K + \frac{{\alpha }_{4}}{\mathrm{log}\left({Hd}_{t + 1}\right)} \\ & \; \end{aligned}$
(7) $ \vdots $
(t + q)年时:
$ \begin{split} & {D}_{i,t + q}={D}_{i,t + q-1} + \mathrm{exp}\Biggr ({\alpha }_{1} + {\alpha }_{2}\mathrm{*}{A}_{t + q-1} + {\alpha }_{3}\mathrm{*}K +\Biggr.\\ & \left.\frac{{\alpha }_{4}}{\mathrm{log}\left({Hd}_{t + q-1}\right)}\right) \end{split} $
(8) 式子中:
$ {D}_{i,t} $ 为 t年时第 i株林木的直径(cm);$ {A}_{t} $ 为 t年时林分的平均年龄;K为7种林分密度指标:包括林分胸高断面积(BA)、优势高营养面积比(Z指数)、株数(N)、相对植距(RS)、林分密度指数(SDI)、相对直径(RD)和SD指数;
Hdt 为t年时的林分优势高;
α1~α4为模型参数;
将林分变量因子,如林分优势高等每年的变化纳入分析,通过建立模型预估对应的林分变量,再将预估出来的林分优势高用来建立杉木单木直径生长模型。林分优势高模型形势如下:
$ {Hd}_{2}=\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{{A}_{1}}{{A}_{2}}\mathrm{*}\mathrm{ln}\left({Hd}_{1}\right) + \left(1-\frac{{A}_{1}}{{A}_{2}}\right)\mathrm{*}\left({\beta }_{1} + {\beta }_{2}\mathrm{*}\frac{{A}_{1}}{{Hd}_{1}}\right)\right) $
(9) 其中β1、β2为待估参数。
本研究中,杉木单木直径模型的参数估计均利用 SAS中非线性回归模块来完成。利用可变生长率法估计模型参数时,应用了循环运算,直到循环停止。
-
林分优势高模型和单木直径生长模型通过统计量平均绝对偏差(MAD)、均方根误差( RMSE)和决定系数(R2) 进行评价。
-
杉木林分优势高模型的参数估计结果及模型的均方根误差、决定系数见表2。从模型结果中参数的标准误差可以得知,模型的参数估计值均为有效值,并且模型的决定系数很高,达到了0.953 9,均方根误差RMSE较小,为1.343 1。因此林分优势高模型可用来预估杉木林分优势高。
表 2 杉木林分优势高模型的参数估计、标准误差、决定系数及均方根误差
Table 2. Parameter estimation, standard error, R2 and RMSE of dominant height model of Chinese fir.
参数
Parameter估计值
Estimate标准误差
Standard dev. error决定系数
R2均方根误差
RMSEβ1 1.583 2 0.360 1 0.953 9 1.343 1 β2 1.470 1 0.325 3 本研究分别用7种不同林分密度指标,利用可变生长率法建立了7种杉木单木直径生长模型,得到的参数估计和标准误差及模型评价见表3。由表3可知,大多数模型参数估计值的标准误差都在接受范围之内,因此模型参数估计值都是有效的。从决定系数R2可以得到模型的拟合效果都相当高,均在0.965以上。7类将密度指标纳入分析的杉木单木直径模型精确度,大部分都高于不含密度指标模型。只有以相对直径RD为密度指标的模型,其决定系数、均方根误差和平均绝对偏差与不含密度指标的模型一致。其次,从模型参数估计α3也可以发现,其标准误比较高,参数估计在0.05水平不显著,相对直径参数估计不稳定。因此可以得到在杉木直径模型中,相对直径RD并不适合作为模型的密度指标。
表 3 不同林分密度指标应用于杉木单木直径生长模型的参数估计及模型评价
Table 3. Parameter estimation and model evaluation of annual tree diameter growth model of Chinese fir with different density indices
密度指标
Density index参数
Parameter估计值
Estimate标准误差
Standard dev. error决定系数
R2平均绝对偏差
MAD均方根误差
RMSE断面积 BA α1 1.630 0 0.038 4 0.971 7 0.513 6 0.837 4 α2 −0.017 9 0.002 0 α3 −0.044 3 0.000 7 α4 −1.486 0 0.050 4 优势高营养面积 Z α1 1.887 4 0.056 8 0.970 6 0.522 4 0.852 5 α2 −0.120 5 0.0018 3 α3 −0.131 1 0.004 9 α4 −0.826 9 0.053 3 每公顷株数 N α1 2.285 6 0.079 2 0.970 5 0.527 5 0.854 7 α2 −0.165 1 0.001 9 α3 −0.000 1 0.000 001 α4 −0.497 8 0.047 4 相对植距 RS α1 0.846 4 0.047 9 0.970 4 0.526 6 0.856 7 α2 −0.158 7 0.001 9 α3 −0.504 3 0.103 0 α4 0.119 3 0.092 8 林分密度指数 SDI α1 2.361 3 0.044 7 0.971 8 0.511 3 0.836 1 α2 −0.049 5 0.001 67 α3 −0.001 1 0.000 02 α4 −1.986 9 0.054 9 相对直径 RD α1 0.996 0 0.042 2 0.967 8 0.530 3 0.856 9 α2 −0.159 1 0.001 9 α3 −0.003 8 0.015 8 α4 −0.291 3 0.044 8 Nilson密度指数 SD α1 1.241 2 0.035 8 0.971 6 0.515 4 0.838 9 α2 −0.008 21 0.002 2 α3 −0.001 5 0.000 02 α4 −1.216 5 0.048 4 不含密度指标 No density α1 0.990 5 0.038 8 0.967 8 0.530 3 0.856 9 α2 −0.159 0 0.001 9 α3 −0.290 0 0.044 7 所有含有密度指标的模型中,模型决定系数最高的为以林分密度指数(SDI)为密度指标的模型,为0.971 8,同时也有最低的平均绝对偏差以及均方根误差,分别为0.511 3、0.836 1。模型精度其次为以林分断面积BA和Nilson密度指数为密度指标的模型,R2分别为0.971 7、0.971 6。其余5种林分密度指标表现介于表现最佳SDI指标(0.971 8)和最差RD指标(0.967 8)之间,所得到的模型精度从大到小依次为林分断面积BA(0.971 7)、Nilson指数SD(0.971 6)、优势高营养面积比Z(0.970 6)、每公顷株数N(0.970 5)和相对植距RS(0.970 4)。
基于最优的含SDI指数建立的单木直径生长模型,绘制了模型残差图。从图1中可以看到,模型在直径较小的时候,如0<D≤5 cm,倾向于低估杉木单木直径生长;在5<D≤20 cm的时候,模型倾向于高估单木直径生长;在D>20 cm的时候,模型则更倾向于低估杉木单木直径生长。总的来说残差均匀分布在0附近,服从正态分布,总体模型情况较好。
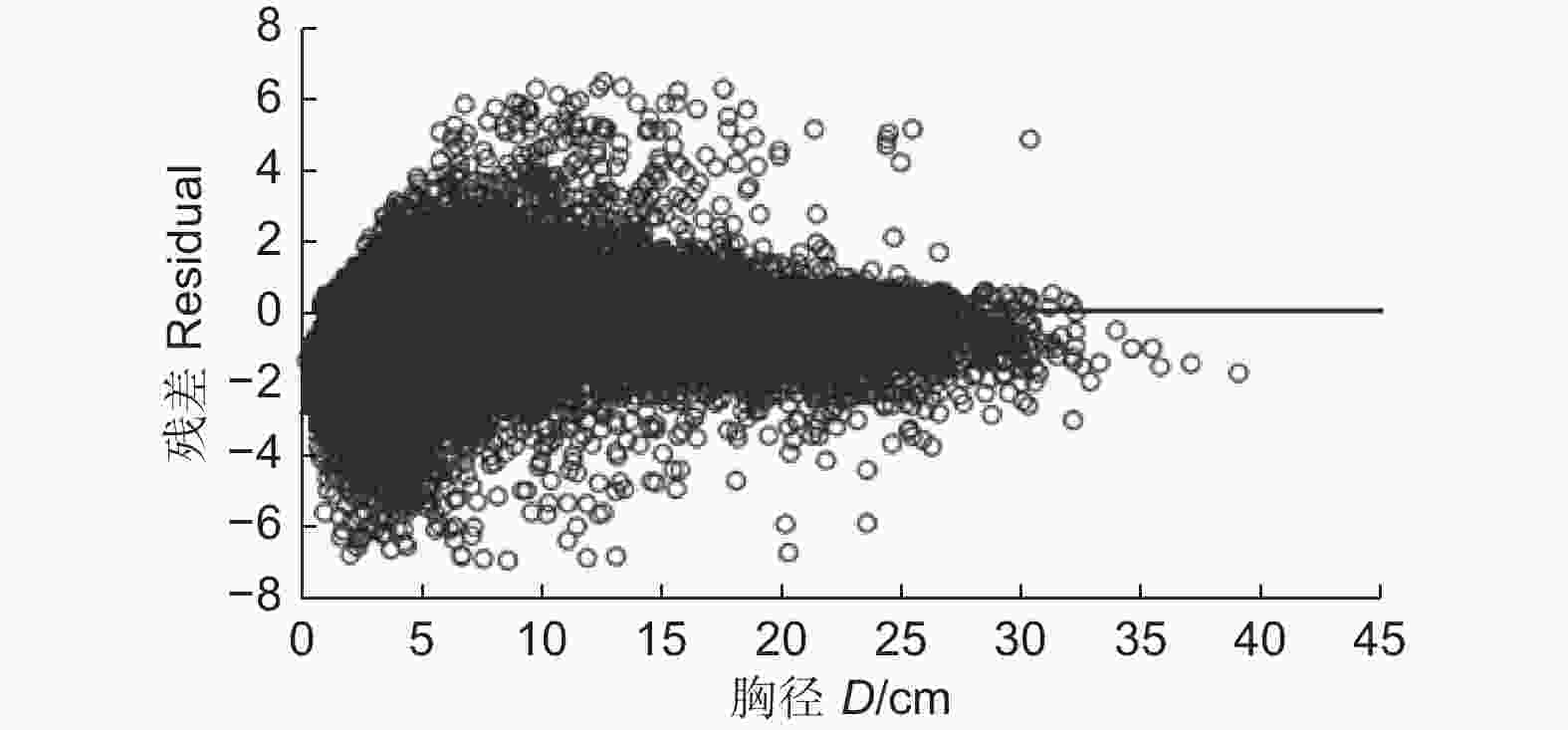
图 1 包含SDI指数的单木直径生长模型的残差分布
Figure 1. Residual distributions of annual tree diameter growth model including SDI
从所有模型的参数估计方面来看,α2在所有模型中均为负值,且α2与林龄A相关,可以看出杉木单木直径增长与年龄在任何密度指数下均呈现负相关关系,即随着林分年龄的增大,单木直径生长量减小。α3在所有模型中均为负值,且是林分密度指标因子的系数,可以得到杉木单木直径生长随着密度指标的增大而减小。α4在所有模型中得到立地估计均为负值,且与林分优势高Hd的倒数负相关,因此随着林分优势高的增大,杉木单木直径生长量增大。林分优势高通常可以代表立地质量,即林分优势高越大立地质量越好,杉木直径生长量也就越大。
-
一般情况在预估单木的年生长量时,主要是基于树干解析中年轮宽度分析[11]。但是利用树干解析分析单木年生长量时需要伐倒树木,而且所选择的解析木一般是选择平均木,并不能完全代表整个林分的生长状况,其次树干解析需要耗费大量的人力物力[12]。近年来,基于已有的连续调查数据,学者研究和利用单木生长模型来预估单木年生长量。例如,为了获得单木年生长量(如胸径、树高和材积),通常用的方法是固定生长率法,其前提是假设在整个生长期,各单木的年生长量是保持不变的。一般常用定期平均生长量来代替年生长量[7]。很明显该估计方法比较简单,并不符合林木的实际生长规律。因为随着森林的演替过程,一些林分的特征(立地,年龄,林分竞争等)和单木本身的一些因子(胸径,树高,冠幅等)都会随着林龄变化而变化,因此也必然会导致单木每年的生长量也发生变化。为解决固定生长率法的缺点,Mcdill和Amateis[13]提出利用内插法来估计单木年生长。之后Cao等[8]也基于内插法模拟单木直径、树高和树冠比的变化,发现内插法比固定生长率法的模拟效果要好的多。然而,内插法的前提是在单木年存活率不变。为进一步提高模型的预测精度,Cao[14]提出了迭代法。该方法比固定生长率法和内插法均表现出明显的优越性,因为该方法考虑了单木在生长期间,林分因子(如竞争和林分优势高)及单木本身的变化而引起的单木直径年生长量的变化。Cao[15] 基于迭代法提出了可变生长率法,该方法也是考虑了林木在生长期间,林分变量如竞争和林分优势高及单木本身的变化而引起的单木胸径年生长量的变化。而且可变生长率法在估计模型参数时,比迭代法简单,计算耗时较少[16]。张雄清等[9]利用可变生长率法构建了油松单木直径和存活率的预估模型,模型拟合效果很好。之后张雄清等[12]基于可变生长率法构建了单木油松年生生长模型,发现该方法不仅能够很好地预测单木断面积生长,而且很好地解决了调查间隔期不一致而导致的相容性情况。
本研究发现密度指标的估计值为负数,说明单木直径生长随着密度的增加而减少。杉木单木的生长主要依靠良好的光照,充沛的水资源以及土壤营养物等,在林分密度增大的情况下,必然会导致树木间对光照、水资源、营养物质等的竞争,竞争的后果则会导致单木直径生长量的减少。即随着竞争强度的增大,树木的生长量会减少,这与之前学者们的结论是一致的[17]。此外表明,用林分密度指数SDI建模预测杉木单木直径生长的模型是最佳选择,这与高启东等[18]研究结果一致。许多学者认为SDI指数的主要优点就是它整合了林分的株树密度和平均直径[19-20]。Zeide[21]报道称在纯林中,SDI指数是最简单而且描述林分密度最有效的一个指标。正是由于SDI指数的优点,多数学者把SDI指数引入生长模型中来表示林分密竞争指标[22-24]。也有学者在生长模型[25]和过程模型[26]中引入了SDI指数并得到了很好的拟合结果。此外,也有学者认为Nilson密度指数(SD)是最优林分密度指标,如车少辉等[27]认为林分密度指数SDI可以与相对植距RS相互转换。模型表现最差的为相对直径RD模型和不含密度指标模型。因此,在构建杉木单木直径生长模型,将相对直径RD以外的林分密度指标纳入模型是非常必要的,可显著提高模型估计的精确度。
-
本研究基于可变生长率法,应用7种不同的林分密度指标以及不含有密度指标,构建得到了8种杉木单木直径年生长模型,模型的拟合精度比较高,R2均在0.96以上。相比较含有密度指标的杉木单木直径模型精度,高于不含密度指标模型。在所有含有密度指标的模型中,决定系数最高的是以林分密度指数(SDI)为密度指标的模型,其次为以林分断面积BA和Nilson密度指数为密度指标的模型。因此,在估计杉木直径年生长量模型时,应该考虑引入Reinek提出的 SDI密度指数,以实现杉木人工林生长的精准预测。
不同林分密度指标在杉木单木直径年生长模型的应用
Annual Tree Diameter Growth Model of Chinese fir Plantations Including Different Stand Density Indices
-
摘要:
目的 分析不同林分密度指标在直径生长模型中的应用,对林分密度的精准管理具有重要意义。 方法 以福建邵武杉木(Cunninghamia lanceolata)人工林密度长期试验林28 a连续观测数据为研究对象,基于可变生长率法,对7种不同的林分密度指标在单木直径年生长模型中的应用进行了比较研究,共构建了8种杉木单木直径年生长模型。 结果 8种模型的拟合精度比较高,R2均在0.96以上。相比较含有密度指标的杉木单木直径模型精度高于不含密度指标模型。在所有含有密度指标的模型中,决定系数最高的是以林分密度指数(SDI)为密度指标的模型,其次为以林分断面积BA和Nilson密度指数为密度指标的模型。 结论 基于SDI林分密度指数构建的杉木单木直径模型最优。 Abstract:Objective To analyze the application value of stand density index in tree diameter growth model for accurate management of stand density. Method Based on the 28 years continuous observation data of the spacing trials of Chinese fir (Cunninghamia lanceolata) plantation in Shaowu, Fujian Province, the annual tree growth model was developed through variable rate method using seven density indices respectively. Also the model without stand density index was developed for comparing. Result All the eight models performed well, with R2 values more than 0.96. The models including the stand density indices were better than the model without stand density index. Among all the models with density indices, the model including stand density index (SDI) has the highest R2 value, followed by the model with stand basal area Ba and SD density index. Conclusion The model including SDI density index performed the best, which provides insights into density management in reason for Chinese fir plantations. -
Key words:
- Chinese fir
- / stand density indices
- / annual tree diameter growth
- / variable rate method
-
表 1 杉木人工林林分和单木变量统计
Table 1. Summary statistics of stand and tree variables of Chinese fir plantation
变量
Variable最小值
Min.最大值
Max.平均值
Mean标准差
Standard deviation林龄 Age/a 4.0 28.0 14.3 7.6 株数 Number of trees/ (tree·hm−2) 1 175.0 10 000.0 4 617.3 2 557.4 优势高 Dominant height/m 2.9 26.9 12.7 6.1 单木胸径 Tree diameter/cm 3.6 39 9.3 5.1 断面积 Stand basal area/(m2·hm-2) 0.8 81.1 39.3 22.2 表 2 杉木林分优势高模型的参数估计、标准误差、决定系数及均方根误差
Table 2. Parameter estimation, standard error, R2 and RMSE of dominant height model of Chinese fir.
参数
Parameter估计值
Estimate标准误差
Standard dev. error决定系数
R2均方根误差
RMSEβ1 1.583 2 0.360 1 0.953 9 1.343 1 β2 1.470 1 0.325 3 表 3 不同林分密度指标应用于杉木单木直径生长模型的参数估计及模型评价
Table 3. Parameter estimation and model evaluation of annual tree diameter growth model of Chinese fir with different density indices
密度指标
Density index参数
Parameter估计值
Estimate标准误差
Standard dev. error决定系数
R2平均绝对偏差
MAD均方根误差
RMSE断面积 BA α1 1.630 0 0.038 4 0.971 7 0.513 6 0.837 4 α2 −0.017 9 0.002 0 α3 −0.044 3 0.000 7 α4 −1.486 0 0.050 4 优势高营养面积 Z α1 1.887 4 0.056 8 0.970 6 0.522 4 0.852 5 α2 −0.120 5 0.0018 3 α3 −0.131 1 0.004 9 α4 −0.826 9 0.053 3 每公顷株数 N α1 2.285 6 0.079 2 0.970 5 0.527 5 0.854 7 α2 −0.165 1 0.001 9 α3 −0.000 1 0.000 001 α4 −0.497 8 0.047 4 相对植距 RS α1 0.846 4 0.047 9 0.970 4 0.526 6 0.856 7 α2 −0.158 7 0.001 9 α3 −0.504 3 0.103 0 α4 0.119 3 0.092 8 林分密度指数 SDI α1 2.361 3 0.044 7 0.971 8 0.511 3 0.836 1 α2 −0.049 5 0.001 67 α3 −0.001 1 0.000 02 α4 −1.986 9 0.054 9 相对直径 RD α1 0.996 0 0.042 2 0.967 8 0.530 3 0.856 9 α2 −0.159 1 0.001 9 α3 −0.003 8 0.015 8 α4 −0.291 3 0.044 8 Nilson密度指数 SD α1 1.241 2 0.035 8 0.971 6 0.515 4 0.838 9 α2 −0.008 21 0.002 2 α3 −0.001 5 0.000 02 α4 −1.216 5 0.048 4 不含密度指标 No density α1 0.990 5 0.038 8 0.967 8 0.530 3 0.856 9 α2 −0.159 0 0.001 9 α3 −0.290 0 0.044 7 -
[1] Dean T J, Baldwin V C. The relationship between Reineke’s stand-density index and physical stem mechanics[J]. Forest Ecology and Management, 1996, 81(1-3): 25-34. doi: 10.1016/0378-1127(95)03666-0 [2] Reineke, L H. Perfecting a stand-density index for even-aged forests[J]. Journal of Agricultural Research, 1933, 46(7): 627-638. [3] Nilson A. Hooldusraiete arvutusliku projekteerimise teooriast[J]. Eesti Po˜llumajanduse Akadeemia tead. to¨o¨de kogumik. Tartu, 1973, 89: 136-142. [4] Nilson A. Modeling dependence between the number of trees and mean tree diameter of stand, stand density and stand sparsity[C]//Cieszewski C J, Strub M. Second International Conference on Forest Measurement and Quantitative Methods and Management & the 2004 Southern Mensurationists Meeting 15–18 June 2004 Hot Springs, Arkansas, USA. University of Georgia, Athens, USA, 74–94. 2006. [5] 刘金福, 王笃志. 福建杉木人工林可变密度收获表编制方法的研究[J]. 林业勘察设计, 1995(2):1-5. [6] Curtis R O. A simple index of stand density for Douglas-fir[J]. Forest Science, 1982, 28: 92-94. [7] 孟宪宇. 测树学(第二版)[M]. 北京: 中国林业出版社, 1996. [8] Cao Q V, Li S S, Mcdill M E. Developing a system of annual tree growth equations for the loblolly pine-shortleaf pine type in Louisiana[J]. Canada Journal Forest Research, 2002, 32(11): 2051-2059. doi: 10.1139/x02-128 [9] 张雄清, 雷渊才. 可变生长率法和固定生长率法在单木年生长预测中的比较研究[J]. 林业科学研究, 2009, 22(6):824-828. doi: 10.3321/j.issn:1001-1498.2009.06.013 [10] Zeide B. Comparison of self-thinning models: an exercise in reasoning[J]. Trees, 2010, 24(6): 1117-1126. doi: 10.1007/s00468-010-0484-z [11] 张惠光. 福建柏单木生长模型的研究[J]. 中南林业调查规划, 2010, 25(4):169-175. doi: 10.1093/wjaf/25.4.169 Curtis R O. Effect of diameter limits and stand structure on relative density indices: a case study[J]. Western Journal of Applied Forestry, 2010, 25(4): 169-175. doi: 10.1093/wjaf/25.4.169 [12] 张雄清. 北京地区油松林分生长、枯损和进界模型的研究 [M]. 北京: 中国林业出版社. 2020. [13] Mcdill M E, Amateis R L. Fitting discrete-time dynamic models having any time interval[J]. Forest Science, 1993, 39(3): 499-519. [14] Cao Q V. Prediction of annual diameter growth and survival for individual trees from periodic measurements[J]. Forest Science, 2000, 46(1): 127-131. [15] Cao Q V. Annual tree growth predictions based on periodic measurements [R]. IUFRO symposium on statistics and information technology in forestry. Blacksburg, VA, 2002: 7-13. [16] Cao Q V, Strub M. Evaluation of four methods to estimate parameters of an annual tree survival and diameter growth model[J]. Forest Science, 2008, 54(6): 617-624. [17] Ford K R, Jan K. Competition alters tree growth response to climate at individual and stand scales[J]. Canadian Journal of Forest Research, 2017, 47: 53-62. doi: 10.1139/cjfr-2016-0188 [18] 高启东, 邓华锋, 程志楚, 等. 蒙古栎间伐林分和未间伐林分生长模型研究[J]. 中南林业科技大学学报, 2014, 34(2):50-54. [19] Ducey M J, Larson B C. Accounting for bias and uncertainty in nonlinear stand density indices[J]. Forst Science, 1999, 45(45): 452-457. [20] Zeide B. Optimal stand density: a solution[J]. Canadian Journal of Forest Research, 2004, 34(4): 846-854. doi: 10.1139/x03-258 [21] Zeide B. How to measure stand density[J]. Trees Structure and Function, 2005, 19(1): 1-14. doi: 10.1007/s00468-004-0343-x [22] Pretzsch H. Grundlagen der Waldwachstumsforschung [M]. Berlin: Blackwell Wissenschafts-Verlag, 2002. 414. [23] Burkhart H E. Comparison of maximum size–density relationships based on alternate stand attributes for predicting tree numbers and stand growth[J]. Forest Ecology and Management, 2013, 289(2): 404-408. [24] Rahman K A, Afizzul M M, Niiyama K, et al. Predicting annual stem diameter increment of major tree species in mixed hill dipterocarp forest with consideration on tree and stand level effects[J]. Journal of Tropical Forest Science, 2016, 28(5): 359-368. [25] Dahlhausen J, Uhl E, Heym M. et al. Stand density sensitive biomass functions for young oak trees at four different European sites[J]. Trees, 2017, 31(6): 1-16. [26] Landsberg J J, Waring R H. A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning[J]. Forest Ecology and Management, 1997, 95(3): 209-228. doi: 10.1016/S0378-1127(97)00026-1 [27] 车少辉, 张建国. 基于自稀疏理论的杉木人工林密度指标研究[J]. 植物研究, 2012, 32(3):343-347. doi: 10.7525/j.issn.1673-5102.2012.03.016 -



 下载:
下载:
















