-
为了解和更新森林资源动态数据库,目前广泛应用的一项重要工具是森林生长与收获模型,它能够预测林木生长变化的量化信息,利用此类模型可以实时优化森林收获调度和调整森林管理规划[1-2]。在构建森林生长模型的研究中,因变量以胸径、树高、优势高和断面积等林分因子为主,自变量一般选择林分年龄。由于林分优势高不仅能够评定林分生长状况及生产力,而且受林分密度影响较小,所以研究林分优势高与林分年龄的关系更受关注[3-5]。
林木年龄作为重要变量,目前获取方法有生长锥法和解析木调查法。生长锥法是由林木髓心开始钻取整个年轮的数据。解析木调查法则需要直接把林木伐倒,按需截取圆盘,通过圆盘查数来获取年轮数据。在热带、亚热带地区或异龄林中,由于自然环境复杂、林分年龄差异较大,林木连续生长或生长停止期较短等原因,其早晚材不易区分,准确的年龄数据不易获得,对于绝大多数阔叶树种和不具有清晰年轮的树种来说,则更是无法获取准确的年轮数据。2种获取林分年龄方法都存在测定困难和年龄不准确的问题,并且2种方法对林木都会造成不可逆的伤害[6-8]。因此,研究建立与年龄无关的生长模型,可以有效避免获取林木年龄困难的问题。
从理论角度出发,诸多学者以经验生长函数为基础模型建立生长模型,这类模型能够清晰地描述因变量与自变量之间的关系,但不能确保单木或林分具有符合生物学特性的生长曲线。理论生长函数从生物学特性角度出发,充分描述生物生长曲线变化趋势,在达到最大生长量后逐渐下降。以理论生长函数为基础模型建立生长模型,能够更好的符合单木或林分的自身生长特性。但当林木或者林分年龄无法获得或不是准确年龄时,通过选择其他林分因子作为自变量,构建与年龄无关的生长模型更为合理。构建与年龄无关的生长模型一般采用代数差分法 (algebraic differenceapproach,ADA)和广义代数差分法( generalized algebraic difference approach,GADA),2种方法以理论生长函数为基础模型,联立方程组消去年龄变量,转换为不含年龄的表达式,以此建立生长模型[9-11]。在保证精度的前提下,目前GADA差分方法构建与年龄无关的生长模型,自变量一般选择容易获取的林分因子,如期初调查的林分数据和多期数据调查的间隔年限等。Richards、Hossfeld IV、Lundqvist-Kolf和Schumacher作为常用的理论生长函数,部分学者则率先基于Richards、Hossfeld IV和Korf理论生长函数为基础模型,构建其差分表达式,选择期初与期末数据作为自变量,分别建立桉树和栎树与年龄无关的单木生长模型,模型精度均有所保证[12-14]。基于我国森林资源连续清查获取的大尺度多期动态数据,葛宏立以Schumacher模型为基础模型,利用GADA方法构建与年龄无关的生长模型,被应用于复位样木的预测与分析[15-16]。基于模型精度角度,差分形式构建的生长模型,其基础方程为一组生长函数,参数可分为公共参数和可变参数,公共参数确保联立的方程组中各因变量与自变量的一致性和有效性,可变参数的选择则可以影响模型的精度。众所周知,气候变化直接影响着林分生长状况,在考虑气候影响时,国红等以Richards为基础模型,分别构建与年龄无关和与年龄有关的生长模型,可变参数则在与温度和降水有关的19个变量中逐步筛选最为敏感的变量,研究表明,与年龄无关的Richards生长模型精度略高于与年龄有关的生长模型,并且在可变参数引入气候因子后,模型精度有明显提高[17]。但是,目前国内外诸多研究主要都基于某一个理论生长函数,构建与年龄无关和与年龄有关的生长模型,比较两者间模型精度。由于每个理论生长函数均有独特的函数性质,比较以多个理论生长函数为基础模型构建的生长模型,综合选择更合适的生长模型尤为重要。
马尾松(Pinus massoniana Lamb.)遍布于华中华南各地,是亚热带地区荒山绿化和造林的主要树种,在我国人工林生态安全和木材产品需求中占有重要位置[18]。本研究以常用的Hossfeld IV、Lundqvist-Kolf、Richards和Schumacher理论生长模型差分形式为基础,建立与年龄无关的马尾松人工林优势高生长模型,研究旨在:1、解决在年龄不可知或者不是有效变量的情况下,马尾松优势高生长预测的问题;2、比较不同年龄无关的理论生长模型在马尾松人工林优势高生长预测中的效果,选择最优年龄无关的生长模型,提高预测精度;3、将参数k和m设定为与地位指数SI相关的可变参数,进一步分析地位指数对与年龄无关的马尾松人工林优势高生长模型的影响。
-
研究区位于广西壮族自治区凭祥市中国林业科学研究院热带林业实验中心,地理位置为 21°57′47″~ 22°19′7″ N,106°39′50″~106°59′30″ E,横跨凭祥市、龙州县和宁明县,与越南、龙州县、宁明县驮龙、寨安乡等地相邻。研究区属于南亚热带半湿润—湿润气候,干湿季节明显,光、水、热资源丰富。年均气候变化鲜明,半年高温多雨,半年温凉少雨,年均降水量为1 200~1 500 mm,年蒸发量为1 261~1 388 mm,相对湿度为80%~84%;年平均气温为20.5~21.7 ℃,最高温度可达到40.3 ℃,最低温度可达到−15 ℃,日照充足。地貌以山地丘陵为主,海拔130~1 046 m,大多数地区分布在500~800 m之间。成土母岩主要有泥质砂岩、砾状灰岩、花岗岩和石灰岩等;土壤主要有红壤、砖红壤。
-
2011年在广西壮族自治区凭祥市中国林业科学研究院热带林业试验中心布设经营单位级森林资源监测样地,样地由半径为6.51 m的3个星状样圆组成,样地总面积为400 m2。对每个样圆内胸径大于5 cm的乔木进行每木检尺,调查并记录树种、胸径、树高、枝下高、冠幅、林木类型、生活力、损伤、干形质量和林木起源,并记录每株树的方位角和距离。
研究选取33块马尾松样地的2期数据(2011年和2015年),样地基本信息如表1所示。马尾松样地的选取原则是:马尾松的胸径断面积超过70%,优势高的计算是通过每块样地最高的3株树的树高取平均得到的[8]。
表 1 样地基本信息
Table 1. Basic information of sample plot
调查时间
Investigation time变量名
Variable平均胸径
Average DBH/cm平均年龄
Average/a平均高
Average H/m优势高
Dominant H/m优势径
Dominant DBH/cm2011 平均值 Mean value 15.24 15.91 14.66 16.85 26.72 标准差 Std deviation 3.86 10.24 2.63 4.42 7.43 最小值 Min value 5.70 5.00 5.18 5.78 6.59 最大值 Max value 21.50 35.00 16.67 23.62 35.18 2015 平均值 Mean value 17.01 15.93 14.68 16.87 26.76 标准差 Std deviation 3.35 10.29 2.56 4.37 7.31 最小值 Min value 8.60 5.00 9.36 11.05 12.73 最大值 Max value 23.30 35.00 16.47 19.54 37.28 -
采用常用的Hossfeld IV、Lundqvist-Kolf、Richards、Schumacher等4个理论生长方程,建模时先由基础方程反解出理论年龄t,引入年龄差a,将t用表达式代替,得到预测年龄(t + a)时的优势树高模型。为了模拟马尾松人工林优势高生长,本研究尝试将生长模型的形状参数m、速度参数k分别作为可变参数。当k或m为可变参数时,分别表达为地位指数的线性函数关系,表达式为:
$ k= {a}_{0} + {a}_{1}\mathrm{*}SI $
(1) $ m= {b}_{0} + {b}_{1}*SI $
(2) 式中,a0、a1、b0、b1是估计参数,SI是地位指数。由Hossfeld IV方程、Lundqvist-Kolf方程、Richards方程和Schumacher方程推导消去年龄因子的优势高生长方程如表2所示。
表 2 基础模型表达式
Table 2. Basic model expression
模型
Model模型名称
Equation表达式
ExpressionM1 Hossfeld差分方程 Yi + 4 = A/(1 + k*((k/((4/Yi)−1))^(1/m) + 4)^(−m)) M2 Richards差分方程 Yi + 4 = A*(1−exp(−4*k)*(1−(Yi/4)^(1−m)))^(1/1−m) M3 Korf差分方程 Yi + 4 = A*exp(−k/((−k/log(Yi/4))^(1/m) + 4)^m) M4 Schumacher差分方程 Yi + 4 = A*exp(−k/4−(k/log(Yi)−log(4))) M5 Hossfeld-k可变参数方程 Yi + 4 = A/(1 + (b0 + b1*SI)*(((b0 + b1*SI)/((4/Yi)−1))^(1/m) + 4)^(−m)) M6 Hossfeld-m可变参数方程 Yi + 4 = A/(1 + k*((k/((4/Yi)−1))^(1/(b0 + b1*SI)) + 4)^(−(b0 + b1*SI))) M7 Richards−k可变参数方程 Yi + 4 = A*(1−exp(−4*(b0 + b1*SI))*(1−(Yi/4)^(1−m)))^(1/1−m) M8 Richards−m可变参数方程 Yi + 4 = A*(1−exp(−4*k)*(1−(Yi/4)^(1−(b0 + b1*SI))))^(1/1−(b0 + b1*SI)) M9 Korf-k可变参数方程 Yi + 4 = A*exp(−(b0 + b1*SI)/((−(b0 + b1*SI)/log(Yi/4))^(1/m) + 4)^m) M10 Korf-m可变参数方程 Yi + 4 = A*exp(−k/((−k/log(Yi/4))^(1/(b0 + b1*SI)) + 4)^(b0 + b1*SI)) M11 Schumacher−k可变参数方程 Yi + 4 = A*exp(−(b0 + b1*SI)/4−((b0 + b1*SI)/log(Yi)−log(4))) M12 Hossfeld基础方程 Y = A/(1 + (k/t^m)) M13 Richards基础方程 Y = A*(1−exp(−k*t))^m M14 Korf基础方程 Y = A*exp(−k/(t^m)) M15 Schumacher基础方程 Y = A*exp(−k/(t) 注: Yi + 4是预测期为4年的单木或平均高,Yi是期初单木或平均高,t是林分年龄,A是当t趋于无穷时的渐近线,k是和生长率相关的参数,m是形状参数。 -
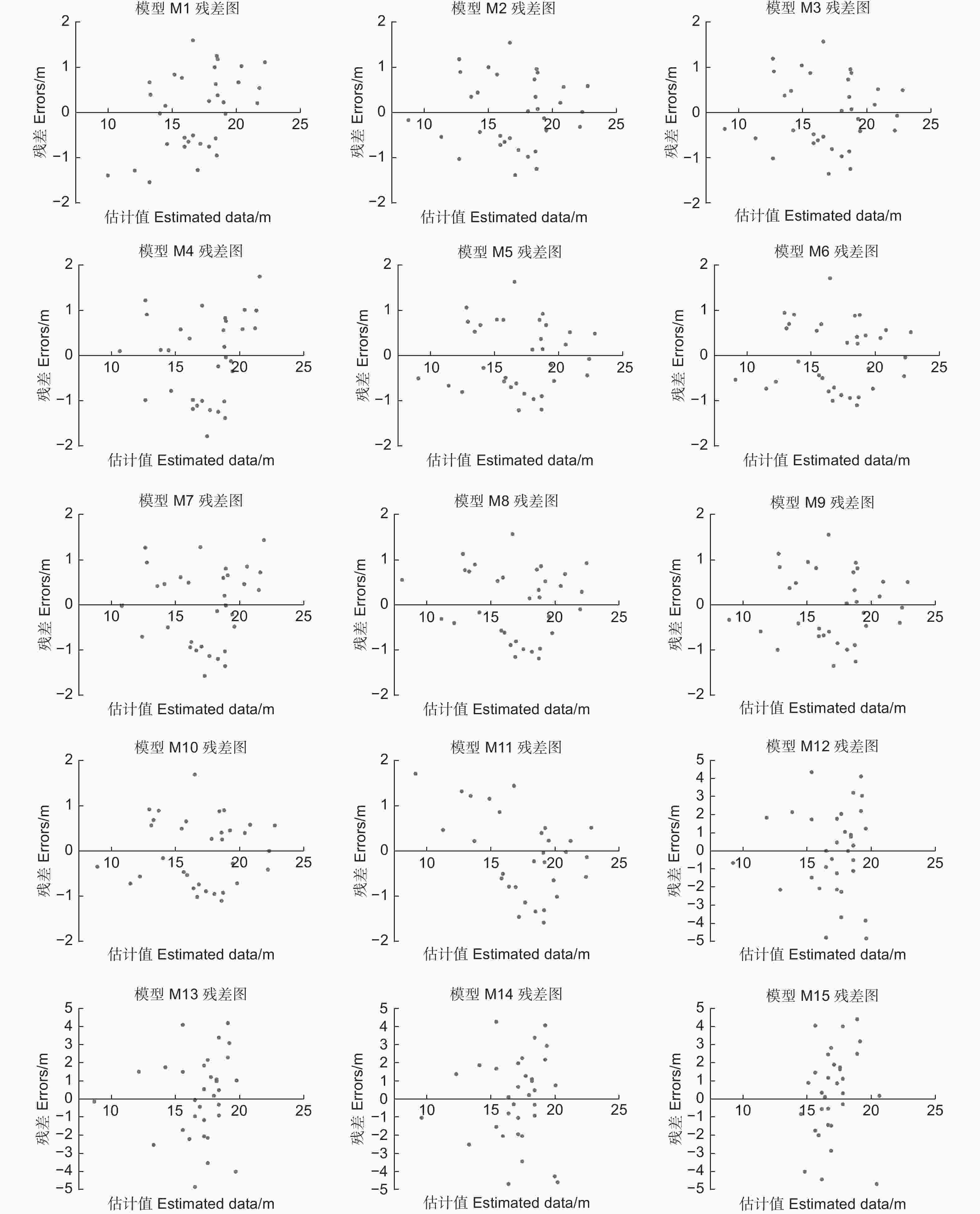
选择均方根误差(RMSE),总相对误差(TRE),确定系数(R2) 3种统计量来检验模型的拟合优度和误差,并观察残差分布是否有异质性,残差均匀分布在x轴两侧说明模型拟合效果好。
-
M1~M15采用最小二乘估计参数值如表3所示,M12渐近线a值为12.05,其他模型的渐近线a值在18.87~35.37之间,其中M1~M4基础模型的渐近线a值在18.77~34.99之间,M5~M10引进地位指数因子模型的渐近线为21.73~35.37。从生物学角度,引进地位指数因子模型更符合马尾松生长特性,而模型M12的渐近线下限只有12.05,明显偏低。
表 3 模型参数
Table 3. Model parameters
模型
Modela k m b0 b1 M1 24.10 40.99 1.512 M2 33.64 0.162 3 1.746 M3 34.99 21.11 0.993 6 M4 18.77 4.871 M5 35.23 1.078 42.120 3 −0.471 0 M6 35.37 29.77 0.892 4 0.008 111 M7 21.73 2.154 0.191 4 0.001 203 M8 23.43 0.032 61 1.973 −0.003 532 M9 33.03 1.136 35.58 −0.094 31 M10 33.7 30.14 0.956 4 0.007 904 M11 30.10 6.462 −0.002 120 M12 12.05 −0.161 5 −0.329 6 M13 19.69 0.151 9 1.202 M14 21.89 3.240 −1.485 M15 22.84 4.329 如表4所示,模型M1~M4为与年龄无关模型,确定系数在0.91~0.94之间,均方根误差RMSE在0.34~0.55,总相对误差1.91%~3.10%,模型M2、M3的确定系数R2、均方根误差RMSE以及相对误差TRE都很接近,但模型M2、M3的R2高于模型M1、M4, RMSE和TRE低于模型M1、M4,模型M2、M3的拟合度优于M1、M4。模型M5、M6相较于M1,模型M5、M6的R2均提高了0.02,模型M5的RMSE和TRE分别降低0.20和1.14%,模型M6的RMSE和TRE分别降低0.13和0.73%,模型拟合优度有明显提高;模型M7、M8相较于M2,模型M7的R2降低0.02,RMSE和TRE分别降低0.03和0.16%,模型M8的R2降低0.01,RMSE和TRE分别提高0.06和0.33%,模型M7的拟合优度有所提高,但不明显;模型M9、M10相较于M3,模型M9的R2、RMSE和TRE变化不大,模型M10的R2无明显提高,但RMSE和TRE分别提高0.08和0.44%,模型拟合优度下降明显;模型M11相较于M4,模型M11的R2、RMSE和TRE无明显变化。模型M12~M15为与年龄有关模型,R2在0.41~0.46,RMSE在0.35~0.42,TRE在2.11%~3.32%,模型M13的R2最高,RMSE和TRE最低,在模型M12~M15中,模型M13拟合度最优。从整体来看,与年龄有关模型M12~M15相较于与年龄无关模型M1~M4,模型M12~M15的R2普遍低于模型M1~M4,而RMSE、TRE则普遍高于模型M1~M4,与年龄无关的模型M1~M4拟合度略优一些。
表 4 模型检验结果
Table 4. Model test results
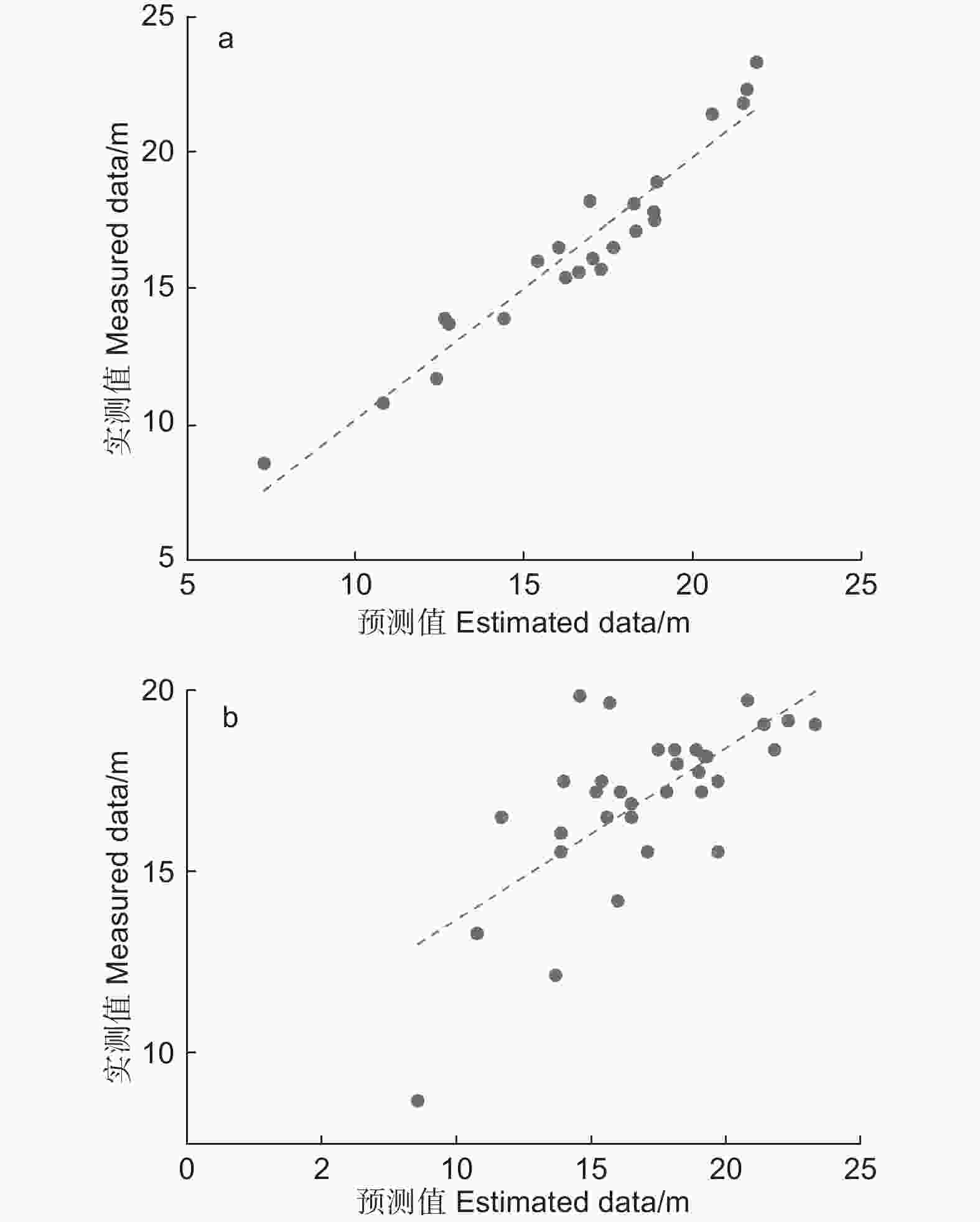
模型 Model R2 RMSE TRE/% M1 0.926 3 0.545 8 3.10 M2 0.942 4 0.340 4 1.92 M3 0.942 2 0.340 3 1.91 M4 0.905 4 0.349 2 1.95 M5 0.944 0 0.348 9 1.96 M6 0.945 2 0.420 5 2.37 M7 0.922 7 0.315 4 1.76 M8 0.934 1 0.398 6 2.25 M9 0.941 1 0.340 8 1.92 M10 0.946 1 0.416 3 2.35 M11 0.841 0 0.327 6 2.01 M12 0.437 2 0.382 8 3.32 M13 0.456 9 0.352 6 2.11 M14 0.436 9 0.420 4 2.47 M15 0.410 8 0.408 6 2.42 如图1所示,图1a和图1b为与年龄无关的模型M3和与年龄有关的模型M13预测值与实测值,存在较为明显的线性关系,模型M3优势高拟合的相关系数高达0.96,模型M13优势高拟合的相关系数仅有0.46。在与年龄无关模型M1~M4的残差图中(图2),模型M2、M3残差分布优于模型M1、M4,与年龄有关模型M12~M15的残差图中,仅M15残差分布图存在明显差距,相较于模型M1~M4,模型M1~M4残差分布更加稳定。引入地位指数后,模型M5、M6相较于模型M1,残差分布更加稳定。
-
准确预测林分生长是掌握林分动态变化的重要步骤。在构建林木生长模型时,诸多学者一般会选择林分年龄作为关键变量,从树木年轮中不仅可以获取准确的年龄,还可以获取连年生长量以及其他的林木信息,但对于人工林来说,期初本底调查是掌握林分信息的有效途径。在针对大多数不具有清晰年轮的树种或林木年龄不是有效变量时,许多学者一般选用相应的期初、期末数据以及已知的年龄间隔构建与年龄无关的生长模型[19],此类模型精度相较于与年龄有关的生长模型,模型精度没有降低,甚至略优[20-22]。以此为基础,邹奕巧等采用单点和双点估计方法构建马尾松与年龄有关和与年龄无关的胸径生长模型,以不同估计方法再次验证与年龄无关的生长模型其精度有保证[23]。本研究以Hossfeld模型、Kolf模型、Richards模型、Schumacher模型为基础模型,构建与年龄有关和与年龄无关的优势高生长模型,同时在差分方程基础上,将地位指数与可变参数建立函数关系带入模型,进一步比较模型精度。
林分优势高生长模型以林分年龄为关键自变量,但获取方法有限,目前只能采用解析木法和生长锥法来获取,但2种方法对林木伤害明显。在针对大多数不具有清晰年轮的树种或林木年龄不是有效变量时,林分或单木的期末与期初调查数据获得相对简单,只需要进行定期固定复测即可。国红等通过比较落叶松平均高与年龄有关的Richards模型和与年龄无关的Richards模型,研究表明与年龄无关的Richards模型预估精度高、误差小,而与年龄有关的Richards方程RMSE和TRE高达1.93和20.48%[17]。高东启等建立蒙古栎天然林与年龄无关的胸径、材积和断面积生长模型,其模型决定系数R2均大于0.98[19]。从诸多研究可知,将年龄变量隐去,其构建的生长模型精度相比于采用年龄变量的模型精度没有降低,甚至略优,因而对于年龄难以获取或者不准确的情况下,采用隐含年龄的模型有助于提高拟合精度。本研究结果表明,与年龄无关模型M1~M4和与年龄有关模型M12~M15相比较,与年龄无关模型M1~M4模型拟合精度更高,一方面可能由于人工林存在较为活跃的补植或砍伐作业,获取的林分年龄不准确,不是有效变量;另一方面与年龄无关模型M1~M4在建模过程中,因变量和自变量为林木自身期初与期末的观测值,几乎没有考虑其他因素带来的影响,如海拔、坡位、环境等。
本研究选择将可变参数k和m均与地位指数建立线性函数关系,地位指数可以综合评价立地与环境因素,在模型M1~M4的基础上,引入地位指数,Hossfeld模型(M5、M6)拟合精度提高,效果最好,其他模型精度提高或降低的幅度不明显,结果表明,Hossfeld模型差分形式在考虑地位指数时,响应程度高于其他3类模型差分形式。通过本研究和参考国红等选用气候因子建立和k的相关关系研究[17],均表明可变参数可以提高模型的拟合精度。在进一步研究中,可考虑建立可变参数和地位指数的非线性函数关系,并且可考虑建立地位指数与参数a的函数关系模型。与年龄无关模型M1~M4中,Richards模型(M2)和Korf模型(M3)拟合效果较好,与年龄有关模型M12~M15中,Richards模型(M13)拟合效果最好。从生物学特性的角度,模型M2、M3和M13拟合的渐近线a值分别为33.64、34.99和19.69,这符合马尾松树高生物学特性生长曲线。在模型M5~M10模型对比中,当k为可变参数时,模型M5、M7、M9拟合精度均高于当m为可变参数时的拟合精度,且相较于模型M1~M4,模型拟合优化效果也高于当m为可变参数时的模型优化效果。进一步表明,在Hossfeld模型、Korf模型以及Richards模型中,地位指数与可变参数k的相关性要高于与可变参数m的相关性,这与Tomè等的结论大体一致[12]。考虑不同林分影响因子或各因子间的交互作用,是提高与年龄无关的生长模型精度的必要手段,需要进一步展开研究,而年龄间隔期作为已知条件也存在较大区别,当树种不同时,树种自身生长特性会导致林木在不同年龄间隔期生长变化出现较大差异。本研究采用的2期数据预测间隔期为4 a,如使用间隔期4 a的3期及以上的多期数据时,其结果是否存在一致性仍需要探讨。邱思玉等研究表明,预测间隔期越短,模型预测精度越高[24]。本研究所用采集数据的预测间隔期为4 a,林木自身生长特性可能导致林木因子在短期内变化较小,使得模型预测误差较小,从而保障模型较高的预测精度。当使用相同间隔年限的多期数据时,建模数据、检验数据均可按等差数列递进方式选取间隔年限较大的数据,进一步分析当预测间隔期较大时,差分方程是否还可以保持较高的预测精度。
-
本研究选用年龄未知的2期固定样地调查数据,以Hossfeld IV、Lundqvist-Kolf、Richards、Schumacher理论生长模型为基础模型,建立与年龄有关和利用其差分形式建立与年龄无关的马尾松人工林优势高生长模型,并在此基础上,建立可变参数k、m与地位指数的线性关系,利用Forstat3.0求解模型参数。与年龄有关的模型中,Richards模型拟合精度最优。与年龄无关的模型中,Richards模型和Korf模型拟合精度高于其他模型。两者相较,与年龄无关模型的拟合精度要高于与年龄有关模型的拟合精度。在考虑地位指数影响时,Hossfeld模型相较于基础模型,模型精度提升最明显。在年龄未知的条件下,构建马尾松林分优势高生长模型,Richards模型、Korf模型以及Hossfeld模型均可作为优先选择模型。
与年龄无关的马尾松优势高生长模型研究
Age-independent Dominant Height Growth Model for Pinus massoniana Plantation
-
摘要:
目的 通过构建与年龄无关的理论生长方程,用于预测在年龄未知或不是有效影响因子时的马尾松人工林优势高。 方法 基于常用的Hossfeld IV、Lundqvist-Kolf、Richards、Schumacher等4个理论生长方程,推导其不含年龄因子的差分形式,构建与地位指数相关的可变参数、与年龄无关的马尾松优势高模型。 结果 在4种基础理论生长模型中,以Richards模型建立的与年龄有关的马尾松人工林优势高生长模型效果最优。与年龄无关模型的拟合精度均高于与年龄有关模型的拟合精度,Richards模型和Korf模型差分形式建立的与年龄无关的马尾松人工林优势高生长模型效果最优。在引入地位指数时,Hossfeld模型的拟合精度提高效果最明显,且以设定k为可变参数时,建立与年龄无关的马尾松人工林优势高生长模型效果最优。 结论 在异龄林或年龄难以获得时,与年龄无关的理论生长模型能够预测优势高的生长,将地位指数与可变参数建立函数关系代入模型拟合后,模型精度提高,可以更好地应用于预测林分生长。 Abstract:Objective An age-independent theoretical growth equation was constructed to predict the dominant height of Pinus massoniana plantation when the age was unknown or not an effective influence factor. Methods Based on the four theoretical growth equations of Hossfeld IV, Lundqvist-Kolf, Richards and Schumacher, an age-independent dominant height model of Pinus massoniana was constructed by using the difference form of hidden age factors, and the free parameters were expressed as a function of site index. Results Among the four basic theoretical growth models, the age-related dominant growth model of Pinus massoniana plantation established by Richards model performed the best. The fitting accuracy of age-independent models was higher than that of age-related models, and the age-independent dominant growth model of Pinus massoniana plantation established by Richards model and Korf model performed the best. When the site index was introduced to the model, the fitting accuracy of Hossfeld model improved most obviously, and when k was set as a variable parameter, the age-independent dominant high growth model was the best. Conclusion When the forest of different age or age is difficult to obtain, the theoretical growth model independent of age can predict the growth of dominant height. After the functional relationship between site index and free parameters is replaced in the model, the accuracy of the model is improved and the model can be better applied to predict stand growth. -
Key words:
- difference equation
- / age-independent method
- / growth model
- / dominant height
-
表 1 样地基本信息
Table 1. Basic information of sample plot
调查时间
Investigation time变量名
Variable平均胸径
Average DBH/cm平均年龄
Average/a平均高
Average H/m优势高
Dominant H/m优势径
Dominant DBH/cm2011 平均值 Mean value 15.24 15.91 14.66 16.85 26.72 标准差 Std deviation 3.86 10.24 2.63 4.42 7.43 最小值 Min value 5.70 5.00 5.18 5.78 6.59 最大值 Max value 21.50 35.00 16.67 23.62 35.18 2015 平均值 Mean value 17.01 15.93 14.68 16.87 26.76 标准差 Std deviation 3.35 10.29 2.56 4.37 7.31 最小值 Min value 8.60 5.00 9.36 11.05 12.73 最大值 Max value 23.30 35.00 16.47 19.54 37.28 表 2 基础模型表达式
Table 2. Basic model expression
模型
Model模型名称
Equation表达式
ExpressionM1 Hossfeld差分方程 Yi + 4 = A/(1 + k*((k/((4/Yi)−1))^(1/m) + 4)^(−m)) M2 Richards差分方程 Yi + 4 = A*(1−exp(−4*k)*(1−(Yi/4)^(1−m)))^(1/1−m) M3 Korf差分方程 Yi + 4 = A*exp(−k/((−k/log(Yi/4))^(1/m) + 4)^m) M4 Schumacher差分方程 Yi + 4 = A*exp(−k/4−(k/log(Yi)−log(4))) M5 Hossfeld-k可变参数方程 Yi + 4 = A/(1 + (b0 + b1*SI)*(((b0 + b1*SI)/((4/Yi)−1))^(1/m) + 4)^(−m)) M6 Hossfeld-m可变参数方程 Yi + 4 = A/(1 + k*((k/((4/Yi)−1))^(1/(b0 + b1*SI)) + 4)^(−(b0 + b1*SI))) M7 Richards−k可变参数方程 Yi + 4 = A*(1−exp(−4*(b0 + b1*SI))*(1−(Yi/4)^(1−m)))^(1/1−m) M8 Richards−m可变参数方程 Yi + 4 = A*(1−exp(−4*k)*(1−(Yi/4)^(1−(b0 + b1*SI))))^(1/1−(b0 + b1*SI)) M9 Korf-k可变参数方程 Yi + 4 = A*exp(−(b0 + b1*SI)/((−(b0 + b1*SI)/log(Yi/4))^(1/m) + 4)^m) M10 Korf-m可变参数方程 Yi + 4 = A*exp(−k/((−k/log(Yi/4))^(1/(b0 + b1*SI)) + 4)^(b0 + b1*SI)) M11 Schumacher−k可变参数方程 Yi + 4 = A*exp(−(b0 + b1*SI)/4−((b0 + b1*SI)/log(Yi)−log(4))) M12 Hossfeld基础方程 Y = A/(1 + (k/t^m)) M13 Richards基础方程 Y = A*(1−exp(−k*t))^m M14 Korf基础方程 Y = A*exp(−k/(t^m)) M15 Schumacher基础方程 Y = A*exp(−k/(t) 注: Yi + 4是预测期为4年的单木或平均高,Yi是期初单木或平均高,t是林分年龄,A是当t趋于无穷时的渐近线,k是和生长率相关的参数,m是形状参数。 表 3 模型参数
Table 3. Model parameters
模型
Modela k m b0 b1 M1 24.10 40.99 1.512 M2 33.64 0.162 3 1.746 M3 34.99 21.11 0.993 6 M4 18.77 4.871 M5 35.23 1.078 42.120 3 −0.471 0 M6 35.37 29.77 0.892 4 0.008 111 M7 21.73 2.154 0.191 4 0.001 203 M8 23.43 0.032 61 1.973 −0.003 532 M9 33.03 1.136 35.58 −0.094 31 M10 33.7 30.14 0.956 4 0.007 904 M11 30.10 6.462 −0.002 120 M12 12.05 −0.161 5 −0.329 6 M13 19.69 0.151 9 1.202 M14 21.89 3.240 −1.485 M15 22.84 4.329 表 4 模型检验结果
Table 4. Model test results
模型 Model R2 RMSE TRE/% M1 0.926 3 0.545 8 3.10 M2 0.942 4 0.340 4 1.92 M3 0.942 2 0.340 3 1.91 M4 0.905 4 0.349 2 1.95 M5 0.944 0 0.348 9 1.96 M6 0.945 2 0.420 5 2.37 M7 0.922 7 0.315 4 1.76 M8 0.934 1 0.398 6 2.25 M9 0.941 1 0.340 8 1.92 M10 0.946 1 0.416 3 2.35 M11 0.841 0 0.327 6 2.01 M12 0.437 2 0.382 8 3.32 M13 0.456 9 0.352 6 2.11 M14 0.436 9 0.420 4 2.47 M15 0.410 8 0.408 6 2.42 -
[1] Amaro A, Reed D, Tome M, et al. Modeling dominant height growth: Eucalyptus plantations in Portugal[J]. Forest Science, 1998, 44(1): 37-46. [2] Sharma R P, Vacek Z, Vacek S, et al. Modelling individual tree diameter growth for Norway spruce in the Czech Republic using a generalized algebraic difference approach[J]. Journal of Forest Science, 2017, 63(5): 227-238. doi: 10.17221/135/2016-JFS [3] 段爱国, 张建国. 杉木人工林优势高生长模拟及多形地位指数方程[J]. 林业科学, 2004, 40(6):13-19. doi: 10.3321/j.issn:1001-7488.2004.06.003 [4] Peter S J, Vanclay J K. Forest site productivity: a review of spatial and temporal variability in natural site conditions[J]. Forestry, 2013, 86(3): 305-315. doi: 10.1093/forestry/cpt010 [5] 雷相东, 朱光玉, 卢 军. 云冷杉阔叶混交过伐林林分优势高估计方法的研究[J]. 林业科学研究, 2018, 31(1):36-41. doi: 10.13275/j.cnki.lykxyj.2018.01.004 [6] Borders B E, Bailey R L, Ware K D. Slash pine site index from a polymorphic model by joining (splining) nonpolynomial segments with an algebraic difference method[J]. Forest Science, 1984, 30(2): 411-423. [7] Vanclay J K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests[M]. CAB International, 1994. [8] 孟宪宇. 测树学[M]. 北京: 中国林业出版社, 2006. [9] Vanclay, Jerome K. Aggregating tree species to develop diameter increment equations for tropical rainforests[J]. Forest Ecology and Management, 1991, 42(3-4): 143-168. doi: 10.1016/0378-1127(91)90022-N [10] Cieszewski C J, Bailey R L. Generalized algebraic difference approach: theory based derivation of dynamic site equations with polymorphism and variable asymptotes[J]. Forest Science, 2000, 46(1): 116-126. [11] Arias-Rodil M, Crecente-Campo F, Barrio-Anta M, et al. Evaluation of age-independent methods of estimating site index and predicting height growth: a case study for maritime pine in Asturias (NW Spain)[J]. European Journal of Forest Research, 2015, 134(2): 223-233. doi: 10.1007/s10342-014-0845-z [12] Tomé J, Tomé M, Barreiro S, et al. Age-independent difference equations for modelling tree and stand growth[J]. Canadian Journal of Forest Research, 2006, 36(7): 1621-1630. doi: 10.1139/x06-065 [13] Gea-Izquierdo G, Cañellas I, Montero G. Site index in agroforestry systems: age-dependent and age-independent dynamic diameter growth models for Quercus ilex in Iberian open oak woodlands[J]. Revue Canadienne De Recherche Forestière, 2008, 38(1): 101-113. [14] Tomé M, Paulo J A. An individual tree growth model for juvenile cork oak stands in southern Portugal[J]. Silva Lusitana, 2009, 17(1): 27-38. [15] 葛宏立, 孟宪宇, 唐小明. 应用于森林资源连续清查的生长模型系统[J]. 林业科学研究, 2004, 17(4):413-419. doi: 10.3321/j.issn:1001-1498.2004.04.002 [16] 葛宏立, 项小强, 何时珍, 等. 年龄隐含的生长模型在森林资源连续清查中的应用[J]. 林业科学研究, 1997, 10(4):420-425. doi: 10.3321/j.issn:1001-1498.1997.04.014 [17] 国 红, 雷渊才, 郎璞玫. 年龄无关的生长模型研究——以落叶松平均高为例[J]. 林业科学研究, 2020, 33(5):129-136. [18] 李亚藏, 冯仲科. 气候敏感的马尾松生物量相容性方程系统研建[J]. 林业科学, 2019, 55(5):66-73. doi: 10.11707/j.1001-7488.20190508 [19] 高东启, 邓华锋, 程志楚, 等. 北京市蒙古栎单木与年龄无关的生长预测模型研究[J]. 福建林学院学报, 2013, 33(4):305-309. doi: 10.3969/j.issn.1001-389X.2013.04.004 [20] Sánchez-González M, Rio M D, Ellas I, et al. Distance independent tree diameter growth model for cork oak stands[J]. Forest Ecology and Management, 2006, 225(1-3): 262-270. doi: 10.1016/j.foreco.2006.01.002 [21] Pukkala T, Lhde E, Laiho O. Growth and yield models for uneven-sized forest stands in Finland[J]. Forest Ecology and Management, 2009, 258(3): 207-216. doi: 10.1016/j.foreco.2009.03.052 [22] Hall K B, Stape J, Bullock B P, et al. A growth and yield model for Eucalyptus benthamii in the Southeastern United States[J]. Forest Science, 2020, 66(1): 25-37. [23] 邹奕巧, 杜 群, 葛宏立. 有年龄生长模型应用于无年龄情况研究[J]. 浙江农林大学学报, 2012, 29(6):889-896. [24] 邱思玉, 曹元帅, 孙玉军, 等. 杉木人工林与年龄无关的优势高生长模型[J]. 南京林业大学学报(自然科学版), 2019, 43(5):121-127. -



 下载:
下载: