-
森林立地质量是林地更新、树种选择、地力维持、生产力评估和经营管理等林业工作和研究的基础[1-2]。作为评价林分生长类型和林地生产力的重要依据,立地质量评价对研究森林生长收获规律、预估林地生产力和制订相应营林措施具有重要的指导意义[3-5]。目前,利用林分生长量的数据来定量评价立地质量的方法包括:地位级法、地位指数法和立地形法等[1, 6]。3种方法分别根据林分平均树高与林分平均年龄、优势木平均高与标准年龄以及优势木平均高与基准胸径的关系来反映立地条件对树高生长的影响。在森林经理经营调查中,由于林分平均高和林分平均年龄是必备调查因子,地位级法被国内外学者广泛关注[7-9]。
传统的地位级表编制方法基于生长模型、误差调整和简单的图形解释虽然能客观反映总体的立地水平及其差异,但采用均值回归模型和标准差调整法编制地位级表对建模数据本身不具有描述性,林分地位级的估测结果可能出现不同程度的高估或低估现象,或者现实林地的生长状况可能根本达不到相应的林分条件平均高[10]。因此,本研究提出一种基于分位数回归模型(Quantile Regression Model)构建地位级表的方法。分位数回归是一种估计因变量或特定分位数函数的完全条件分布的方法,由Koenker等人[11]提出,是统计学和计量经济学常用的回归分析方法之一[12]。一般的均值回归估计方法仅针对协变量的条件均值或中心效应[13],而分位数回归方法可灵活地描述相应条件分位数自变量和因变量之间关系并得到的回归曲线。目前,分位数回归模型已被应用于多个林业研究中,如:森林资源量的估算[14],林分密度[15],直径分布预测[16],直径增长[17],削度[18]和森林的地上生物量[19]等。
根据分位数模型可得出各分位数对应的条件估计值和不易受到极端值影响的特点,该模型可用于描述树高生长过程与立地质量的关系[20-21],但目前该模型在立地质量评价研究中鲜有报道。基于此,本研究以福建省三明市将乐国有林场的杉木(Cunninghamia lanceolata (Lamb.) Hook.)纯林为例,构建基于分位数回归模型的地位级表,并与标准差调整法进行比较,对将乐县国有林场立地质量进行评价与分析,为进一步提高地位级分级策略的效率和立地质量评价的准确性提供理论依据和参考。
-
数据来源于福建省三明市将乐国有林场2012至2017年期间调查的418块杉木纯林小班调查样地数据,主要分布于将乐县南口乡、完全乡、黄潭镇、白莲镇、水南镇、余坊乡、光明乡和古镛镇。样地均为面积0.06 hm2的方形样地。主要调查内容包括各样地地理坐标、坡度、坡向、坡位、海拔等地形因子,土壤类型、土壤厚度、腐殖质层厚度等土壤因子,每木检尺测定样地内每株树木的胸径、树高、冠幅等,通过计算得出各样地的林分平均年龄、林分平均胸径、林分平均树高等林分因子。样地各龄级的信息统计见表1。
表 1 各龄级样地基本信息
Table 1. Summary of basic information statistics of sample plots for each age-class
龄级
Age class样地数
Plot number平均年龄
Mean age /a平均树高
Mean height /m树高最小值
Min. height /m树高最大值
Max. height /m树高标准差
Height standard deviation /m2 53 7.92 6.38 1.60 10.20 1.44 3 12 11.00 8.28 6.30 13.20 1.88 4 9 18.11 11.23 6.50 15.40 2.60 5 95 23.71 13.91 6.80 19.30 2.71 6 137 28.66 14.94 10.20 20.70 1.94 7 82 32.06 15.76 9.20 22.30 2.61 8 13 38.69 16.18 9.30 20.10 2.90 9 8 42.63 15.89 11.30 19.80 2.43 10 5 47.60 15.42 13.30 16.80 1.22 11 4 53.25 13.75 9.20 16.30 2.75 注:杉木人工林为每5年1个龄级。
Note: 5 years per an age class for Chinese fir. -
基于已有的研究成果选择了7个常用的生长模型(表2)作为基础模型[22-25]。
表 2 基础树高生长模型
Table 2. Basic height growth models
模型号
Models类型
Types表达式
FunctionMod.1 Line $ y=a+b\cdot x $ Mod.2 Weibull $ y=1.3+a\cdot (1-\mathrm{e}\mathrm{x}\mathrm{p}(-b*{x}^{c}\left)\right) $ Mod.3 Schumacher $ y=1.3+\mathrm{e}\mathrm{x}\mathrm{p}(a+b\cdot {x}^{c}) $ Mod.4 Logistic $ y=1.3+a/(1+b\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-c\cdot x\left)\right) $ Mod.5 Logistic $ y=1.3+a/(1+b^-1\cdot {x}^{-c}) $ Mod.6 Richards $ y=1.3+a\cdot {(1-\mathrm{e}\mathrm{x}\mathrm{p}(-b\cdot x\left)\right)}^{c} $ Mod.7 Gompertz $ y=1.3+a\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-b\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-c\cdot x\left)\right) $ 注:y为林分平均树高;x为林分平均年龄;a,b,c为模型参数。
Note: y is the average tree height of the forest stand; x is the average age of the forest stand; a, b, and c are the model parameters.为了比较模型的拟合优度,用赤池信息准则(AIC)、贝叶斯信息准则(BIC)、对数似然值(logLik)、均方根误差(RMSE)、决定系数(R2)和平均绝对误差(MAE),选择拟合模型,所有计算均使用R(Version 3.6.1)软件进行。
-
以导向曲线为基础,按标准年龄时树高值和地位级距(C),采用标准差调整法,可形成地位曲线簇(即树高生长曲线簇)[1]。杉木在25 a左右树高生长区域稳定,且杉木在20~30 a时达到数量、经济成熟龄[26]。因此,本研究以林分树高生长量趋于稳定、杉木达到成熟龄确定基准年龄(A0)为25 a。
(1)拟合各龄级树高标准差方程
根据各龄级树高标准差(SH)与龄级平均年龄(Ai),利用SH=a+b × lg(Ai)式拟合龄级树高标准差方程。将各龄级代入,计算出各龄级树高标准差理论值(
$ {S}_{A} $ )。本研究方程为:$ {S}_{H}=-0.307\;1+1.74\;0 9\times \mathrm{l}\mathrm{g}\left({A}_{i}\right) $
(2)导算地位级表
通常在基准年龄(A0)时,由于导向曲线的理论树高值可能不是地位级数值,因此需要根据基准年龄时的树高(H0)与标准差理论值(S0)的大小进行调整,公式如下:
$ {H}_{ij}={H}_{ik}\pm \left[\left(\frac{{H}_{0j}-{H}_{0k}}{{S}_{{A}_{0}}}\right)\cdot {S}_{{A}_{i}}\right] $
式中,Hij为第i龄级第j地位级调整后的树高;Hik为第i龄级的导向曲线树高;H0j为基准年龄时第j地位级的树高;H0k为基准年龄时导向曲线树高;
$ {S}_{{A}_{0}} $ 为基准年龄所在龄级树高标准差理论值;$ {S}_{{A}_{i}} $ 为第i龄级树高标准差理论值。若将
$ {H}_{j}=\dfrac{{H}_{0j}-{H}_{0k}}{{S}_{A0}} $ 称为调整系数时,原式可化简为:$ {H}_{ij}={H}_{ik}\pm {H}_{j}{S}_{{A}_{i}} $
以调整后的导向曲线为准,按地位级距C逐龄级导算出各地位级曲线上的树高值,其余地位级的调整系数Kj为:
$ {K}_{j}=\frac{C}{{S}_{A0}} $
-
分位数回归模型基于表2中的线性和非线性模型来预测第τ分位数的树高模型:
$ \widehat{{y}_{\tau }}\left(x\right)=f\left(\mathrm{x}\right) $
式中:
$ \widehat{{y}_{\tau }}\left(x\right) $ 是树高的第τ分位数的预测值。与最小二乘方法相比,分位数回归模型的参数通过最小化分位回归领域的损失函数(或称为检验函数)获得[27]。
$ \mathrm{m}\mathrm{i}\mathrm{n}\left\{\sum _{y\ge \widehat{{y}_{\tau }}\left(x\right)}\tau \left[y-\widehat{{y}_{\tau }}\left(x\right)\right]+\sum _{y<\widehat{{y}_{\tau }}\left(x\right)}\left(1-\tau \right)\left[\widehat{{y}_{\tau }}\left(x\right)-y\right]\right\} $
在本研究中,分位数回归模型的构建通过使用R语言中的“quantreg”包来完成[28]。
-
计算每个样地林分平均高与各分级曲线树高预测值的差值平方和(或差值的绝对值),以确定每个样地的地位级,具有最小残差平方和的模型即为该样地所属的立地类型,从而确定该林分目前的地位级。分别采用传统方法与分位数回归模型方法统计出每个林分的地位级,对分级结果进行比较和差异分析。
-
根据数据资料整理,采用最小二乘法和非线性拟合技术拟合7个基础模型,其拟合结果如表3。依据AIC、BIC、RMSE和MAE最小,logLik和R2值最大的原则,选出最优模型Mod.4(Logistic)为最优导向曲线方程:
表 3 导向曲线模型拟合结果汇总
Table 3. Fitting statistics for Guide curve growth models
模型
Model赤池信息准则
AIC贝叶斯信息准则
BIC对数似然比
logLik均方根误差
RMSE决定系数
R2平均绝对误差
MAEMod.1 2129.693 2142.007 −1061.85 2.589 0.604 1.971 Mod.2 2021.579 2033.893 −1007.79 2.295 0.689 1.721 Mod.3 2035.125 2051.544 −1013.56 2.324 0.681 1.765 Mod.4 2002.565 2018.984 −997.282 2.241 0.703 1.648 Mod.5 2026.534 2042.953 −1009.27 2.302 0.687 1.740 Mod.6 2019.778 2036.197 −1005.89 2.285 0.692 1.718 Mod.7 2009.539 2025.958 −1000.77 2.259 0.699 1.677 注:加粗字体为最优模型统计量
Note: The bold font is the optimal model statistic$ H=1.3+15.016/(1+5.221\times \mathrm{e}\mathrm{x}\mathrm{p}(-0.139\times A\left)\right) $
-
(1)基准年龄及地位级距
根据基准年龄确定条件,本研究中杉木的标准年龄为25 a。杉木达到基准年龄时基准树高H0为14.24 m,树高变动范围为6.8~19.3 m。根据将乐地区杉木的编表资料,以及树高、胸径的绝对变动幅度和经营水平,确定地位级距C为2 m,即地位级H0j分别为6至20的8个地位级。
(2)地位级表的编制
标准年龄A0(25 a)代入导向曲线方程得到树高理论值H0k(14.24 m)并计算调整系数Kj和各相应龄级树高值绘制地位级表(表4)。根据立地级表和导向曲线方程拟合8个地位级的生长趋势模型(图1),模型参数及统计量如表5。
表 4 杉木人工林地位级及相应树高
Table 4. Site class and corresponding tree height of Chinese fir
地位级
Site class龄级 Age class 2 3 4 5 6 7 8 9 10 11 6 1.27 3.02 4.75 6.00 6.72 7.08 7.22 7.26 7.24 7.20 8 2.86 4.81 6.67 8.00 8.78 9.18 9.36 9.42 9.42 9.40 10 4.46 6.61 8.59 10.00 10.84 11.28 11.50 11.58 11.61 11.61 12 6.05 8.41 10.51 12.00 12.90 13.39 13.63 13.75 13.79 13.81 14 7.65 10.20 12.43 14.00 14.96 15.49 15.77 15.91 15.98 16.01 16 9.24 12.00 14.34 16.00 17.01 17.59 17.90 18.07 18.17 18.22 18 10.83 13.80 16.26 18.00 19.07 19.69 20.04 20.24 20.35 20.42 20 12.43 15.59 18.18 20.00 21.13 21.79 22.17 22.40 22.54 22.63 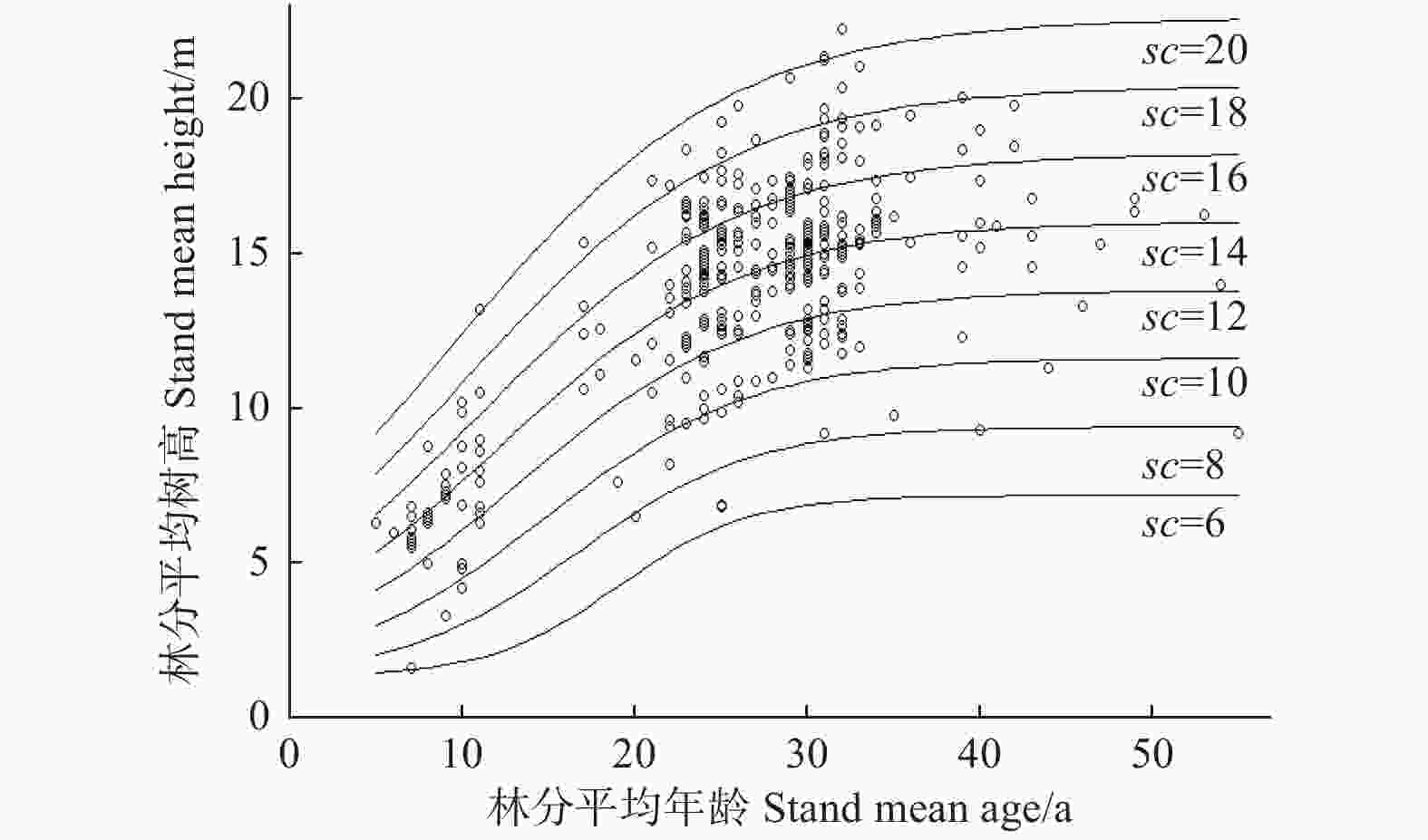
图 1 传统方法的地位级分布和建模数据散点分布
Figure 1. Distribution of site classes by traditional method and scatter plot of modeling data
表 5 地位级模型参数及统计量
Table 5. Parameter estimation and fitting statistics for site class models
地位级
Site class系数
Parameter系数预测值
EstimateP值
P value地位级
Site class系数
Parameter系数预测值
EstimateP值
P value6 a 5.880 <0.001 14 a 14.751 <0.001 b 155.907 0.123 b 5.386 <0.001 c 0.265 0.0001 c 0.140 <0.001 8 a 8.109 <0.001 16 a 16.957 <0.001 b 26.642 <0.001 b 4.305 <0.001 c 0.197 <0.001 c 0.133 <0.001 10 a 10.330 <0.001 18 a 19.162 <0.001 b 11.760 <0.001 b 3.630 <0.001 c 0.167 <0.001 c 0.128 <0.001 12 a 12.543 <0.001 20 a 21.366 <0.001 b 7.351 <0.001 b 3.171 <0.001 c 0.151 <0.001 c 0.124 <0.001 -
地位等级通常分成5~7级,为便于与传统地位级表编制方法比较,本研究分位数回归模型的地位级表也分为8个地位级。根据数据的分布和导向曲线方程(Logistic模型)选择了8个分位数(0.01、0.05、0.15、0.30、0.70、0.85、0.95、0.99)(图2)。其中,分位数0.01和0.99接近于地位级的下限和上限,可作为地位级Ⅷ和Ⅰ,分位数0.05和0.95是研究区地位级的最前5%和最后5%水平,分别记作地位级Ⅶ和Ⅱ,分位数0.15、0.30、0.70、0.85则依据数据的分布状况以及保持分位数回归曲线簇形状的相对均匀,分别记作地位级Ⅵ、Ⅴ、Ⅳ和Ⅲ,模型参数统计结果(表6)。
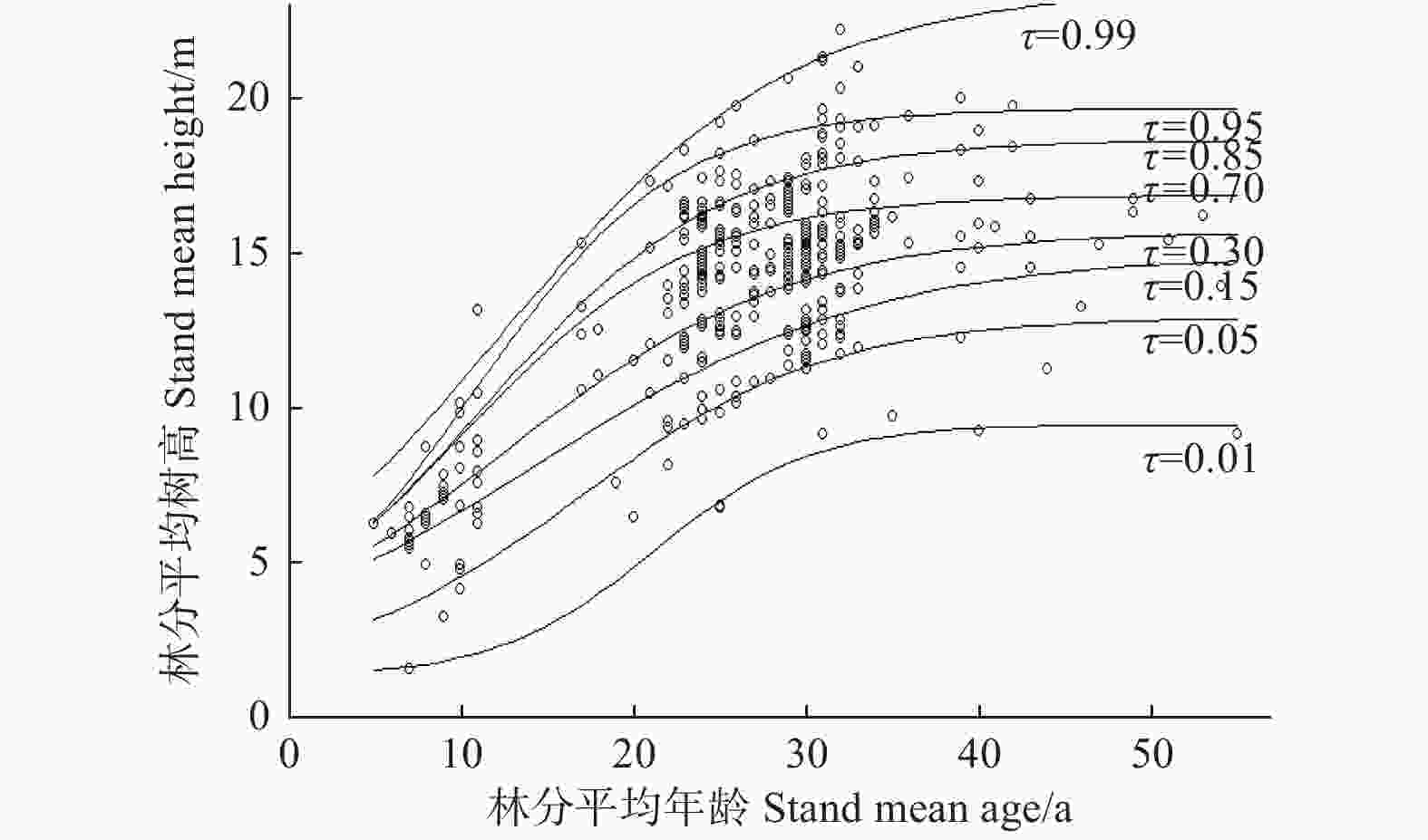
图 2 分位数回归方法的地位级分布和建模数据散点分布
Figure 2. Distribution of site classes by quantile regression method and scatter plot of modeling data
表 6 分位数回归模型参数及统计量
Table 6. Parameter estimation and fitting statistics for quantile regression models of site class
地位级
Site class分位数(τ)
Quantile系数
Parameters系数预测值
EstimateP值
P value地位级
Site class分位数(τ)
Quantile系数
Parameters系数预测值
EstimateP值
P valueⅧ 0.01 a 8.192 <0.001 Ⅳ 0.70 a 15.624 <0.001 b 105.787 0.782 b 4.480 <0.001 c 0.220 0.186 c 0.149 <0.001 Ⅶ 0.05 a 11.670 <0.001 Ⅲ 0.85 a 17.412 <0.001 b 10.553 0.046 b 5.112 <0.001 c 0.140 <0.001 c 0.145 <0.001 Ⅵ 0.15 a 13.698 <0.001 Ⅱ 0.95 a 18.427 <0.001 b 4.315 <0.001 b 6.256 <0.001 c 0.102 <0.001 c 0.171 <0.001 Ⅴ 0.30 a 14.457 <0.001 Ⅰ 0.99 a 22.284 <0.001 b 4.350 <0.001 b 4.384 0.008 c 0.119 <0.001 c 0.119 <0.001 -
从两种方法的地位级分级过程看,传统方法地位级分级曲线规则,能够反映出林分地位级的普遍规律,得到的地位级表示基准年龄时的林分平均高。而分位数回归的8个分位数点的选择是根据建模数据分布来确定的,地位级分级结果反映出的是不同特定条件下的变化规律。因此,拟合的分级曲线可能存在过于接近的现象,基准年龄较小时无法直接判断地位级分级状况,造成对地位级分级结果模糊或对普遍规律的理解不足的现象。
利用各模型的最小残差平方和来判断418块样地的地位级状况,从两种方法的分级结果(表7)可以看出,传统地位级表中大多数样地地位级分布于10至16地位级,与分位数回归模型中多数样地分级分布于Ⅵ至Ⅲ地位级结果基本一致。对两种分级结果进行差异显著性检验,分位数回归模型的地位级分级效果与传统方法没有显著差异(F值0.130 3,P值0.719 3),表明分位数回归模型能够较为准确的描述研究区内林分的地位级的分布特征。两种方法分级的主要差异在于对最大和最小地位级的分级表现,分位数回归方法将更多的样地划分到最大和最小地位级中,反映了研究区各龄级林分平均高的完整分布状况。总体而言,传统方法的拟合曲线表现出的是平均状态和预设的变化规律,而分位数回归模型利用数据分布特征所反映出的是特定状态和条件对应的变化规律,其划分的地位级结果在很大程度上取决于建模样本的结构和数据质量。
表 7 传统方法(左)和分位数回归模型(右)对样地地位级分级的结果
Table 7. The result of site classes grouped by traditional method (left) and quantile regression model (right)
地位级
Site class龄级 Age class 地位级
Site class龄级 Age class 2 3 4 5 6 7 8 9 10 11 2 3 4 5 6 7 8 9 10 11 6 1 0 1 3 0 0 0 0 0 0 Ⅷ 1 0 1 3 0 2 1 0 0 1 8 2 0 1 5 1 2 1 1 0 1 Ⅶ 6 0 1 11 11 4 1 1 1 0 10 5 1 0 11 20 11 1 0 1 0 Ⅵ 10 4 0 5 16 12 0 2 0 1 12 16 6 3 16 32 23 4 3 2 2 Ⅴ 30 5 3 20 39 21 4 2 2 1 14 26 3 2 30 57 26 3 2 2 1 Ⅳ 3 1 2 26 43 21 2 1 2 1 16 3 1 1 25 24 13 4 2 0 0 Ⅲ 0 0 1 23 25 7 3 1 0 0 18 0 0 1 5 3 6 0 0 0 0 Ⅱ 3 1 0 4 1 11 2 1 0 0 20 0 1 0 0 0 1 0 0 0 0 Ⅰ 0 1 1 3 2 4 0 0 0 0 -
本研究提出一种基于分位数回归模型的立地质量分级和评价方法,以福建省三明市将乐县国有林场小班调查样地数据构建基于分位数回归模型的地位级分级模型,并与传统地位级划分方法相比较。结果表明,基于不同分位数拟合曲线簇,可准确评估林地地位级水平;根据林分平均高与各分级曲线树高预测值的差值平方和(或差值绝对值)最小的原则,可迅速确定该林分的地位级和生长类型,实现快速、准确的立地质量评价,为精准评估森林生产力和进一步提升森林质量评价效率提供方法和依据。
我国森林资源清查数据中主要记录平均木的树高,采用林分平均树高构建地位级表可以使分位数回归方法与森林清查数据兼容。资源清查的小班调查数据虽然没有标准地调查数据准确,但其数据量大且覆盖广,能够从一定程度上反映立地质量对林分生产力的影响[7]。分位数回归模型可描述、分类、预测和验证小班数据林分生长与地位级之间的关联性,基于导向生长模型的分位数回归曲线簇能够更直观的反映出不同地位级下杉木树高的变化轨迹,从整体上描述了各小班林地生产力,并有效地简化了地位级划分的测算工作。因此,结合分位数回归方法和森林资源连续清查数据构建林分尺度和区域尺度的地位级分级体系,可以实现对数据的充分利用。但是,由于分位数回归模型受数据分布的影响,地位级的划分结果很大程度上取决于建模样本的结构和数据质量。今后的研究中需要考虑地位级划分和分位点选择的联系,以进一步提高分位数回归模型在生产力评价中的适用性。
基于分位数回归的杉木人工林地位级划分方法研究
Site Classes Grouping Method Based on Quantile Regression of Chinese Fir Plantations
-
摘要:
目的 优化地位级划分策略的效率并提高立地质量分级的准确性,提出基于分位数回归模型的地位级模型和立地质量评价方法。 方法 分别采用标准差调整法和分位数回归方法分级并评价了福建省三明市将乐国有林场418个杉木纯林样地的立地质量,并将结果进行比较。具体为:以林分树高生长量趋于稳定和杉木达到成熟龄为标准确定基准年龄(A0)。采用标准差调整法并按标准年龄时树高值和地位级距构建地位级曲线簇,并划分了8个地位级。采用分位数回归法以导向曲线为基础,根据数据分布特点,指定8个分位点(0.01,0.05,0.15,0.30,0.70,0.85,0.95,0.99)构建分位数回归模型,并以分位数曲线划分地位级。 结果 根据林分平均高与各分级曲线树高预测值的差值平方和(或差值绝对值)最小的原则,分位数回归模型在林地地位级划分方面虽与传统方法无显著差异,却显著提高了划分效率,并准确地实现了对杉木人工纯林地位级的评价。 结论 分位数回归模型可描述、分类、预测和验证林分生长与地位级之间的关联性,基于导向生长模型的分位数回归曲线簇能够更直观地反映出不同地位级下杉木树高的变化规律,从而全面准确地预测杉木人工林的生产力水平。 Abstract:Objective To optimize the efficiency of the site classes grouping strategy and improve the accuracy of site classification, site classes grouping model and to propose a site quality evaluation method based on quantile regression model. Method The traditional methods (standard deviation adjustment method) and quantile regression method were used to classify and evaluate the site quality of 418 pure Chinese fir (Cunninghamia lanceolata) forests at Jiangle Forest Farm in Sanming City, Fujian Province, and the results were compared. The baseline age (A0) was determined based on the high growth of the stand tree and the maturity of the Chinese fir plantations. Using standard deviation adjustment method and according to the standard age tree height value and exponential interval, the site classes curve cluster was constructed and divided into 8 levels. The quantile regression method was based on the guiding curve. According to the data distribution characteristics, 8 quantile points (0.01, 0.05, 0.15, 0.30, 0.70, 0.85, 0.95, and 0.99) were specified to construct the quantile regression model, and the quantile curves were used to divide the site classes. Result The results showed that the quantile regression model could quickly and accurately determine the site type of the pure Chinese fir plantation, based on the principle that the sum of squares (or the absolute value of the difference) between the average stand height and the prediction stand height of each site class curves is the smallest. The evaluation results of the site quality were not significantly different from the traditional methods. Conclusion The quantile regression model describes, classifies, regresses, predicts and verifies the correlation between stand growth and site quality from the perspective of data. The quantile regression curve cluster, based on the guided growth model, intuitively reflect the stand high changing under the different site class, so as to comprehensively and accurately predict the productivity of Chinese fir plantations. -
表 1 各龄级样地基本信息
Table 1. Summary of basic information statistics of sample plots for each age-class
龄级
Age class样地数
Plot number平均年龄
Mean age /a平均树高
Mean height /m树高最小值
Min. height /m树高最大值
Max. height /m树高标准差
Height standard deviation /m2 53 7.92 6.38 1.60 10.20 1.44 3 12 11.00 8.28 6.30 13.20 1.88 4 9 18.11 11.23 6.50 15.40 2.60 5 95 23.71 13.91 6.80 19.30 2.71 6 137 28.66 14.94 10.20 20.70 1.94 7 82 32.06 15.76 9.20 22.30 2.61 8 13 38.69 16.18 9.30 20.10 2.90 9 8 42.63 15.89 11.30 19.80 2.43 10 5 47.60 15.42 13.30 16.80 1.22 11 4 53.25 13.75 9.20 16.30 2.75 注:杉木人工林为每5年1个龄级。
Note: 5 years per an age class for Chinese fir.表 2 基础树高生长模型
Table 2. Basic height growth models
模型号
Models类型
Types表达式
FunctionMod.1 Line $ y=a+b\cdot x $ Mod.2 Weibull $ y=1.3+a\cdot (1-\mathrm{e}\mathrm{x}\mathrm{p}(-b*{x}^{c}\left)\right) $ Mod.3 Schumacher $ y=1.3+\mathrm{e}\mathrm{x}\mathrm{p}(a+b\cdot {x}^{c}) $ Mod.4 Logistic $ y=1.3+a/(1+b\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-c\cdot x\left)\right) $ Mod.5 Logistic $ y=1.3+a/(1+b^-1\cdot {x}^{-c}) $ Mod.6 Richards $ y=1.3+a\cdot {(1-\mathrm{e}\mathrm{x}\mathrm{p}(-b\cdot x\left)\right)}^{c} $ Mod.7 Gompertz $ y=1.3+a\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-b\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-c\cdot x\left)\right) $ 注:y为林分平均树高;x为林分平均年龄;a,b,c为模型参数。
Note: y is the average tree height of the forest stand; x is the average age of the forest stand; a, b, and c are the model parameters.表 3 导向曲线模型拟合结果汇总
Table 3. Fitting statistics for Guide curve growth models
模型
Model赤池信息准则
AIC贝叶斯信息准则
BIC对数似然比
logLik均方根误差
RMSE决定系数
R2平均绝对误差
MAEMod.1 2129.693 2142.007 −1061.85 2.589 0.604 1.971 Mod.2 2021.579 2033.893 −1007.79 2.295 0.689 1.721 Mod.3 2035.125 2051.544 −1013.56 2.324 0.681 1.765 Mod.4 2002.565 2018.984 −997.282 2.241 0.703 1.648 Mod.5 2026.534 2042.953 −1009.27 2.302 0.687 1.740 Mod.6 2019.778 2036.197 −1005.89 2.285 0.692 1.718 Mod.7 2009.539 2025.958 −1000.77 2.259 0.699 1.677 注:加粗字体为最优模型统计量
Note: The bold font is the optimal model statistic表 4 杉木人工林地位级及相应树高
Table 4. Site class and corresponding tree height of Chinese fir
地位级
Site class龄级 Age class 2 3 4 5 6 7 8 9 10 11 6 1.27 3.02 4.75 6.00 6.72 7.08 7.22 7.26 7.24 7.20 8 2.86 4.81 6.67 8.00 8.78 9.18 9.36 9.42 9.42 9.40 10 4.46 6.61 8.59 10.00 10.84 11.28 11.50 11.58 11.61 11.61 12 6.05 8.41 10.51 12.00 12.90 13.39 13.63 13.75 13.79 13.81 14 7.65 10.20 12.43 14.00 14.96 15.49 15.77 15.91 15.98 16.01 16 9.24 12.00 14.34 16.00 17.01 17.59 17.90 18.07 18.17 18.22 18 10.83 13.80 16.26 18.00 19.07 19.69 20.04 20.24 20.35 20.42 20 12.43 15.59 18.18 20.00 21.13 21.79 22.17 22.40 22.54 22.63 表 5 地位级模型参数及统计量
Table 5. Parameter estimation and fitting statistics for site class models
地位级
Site class系数
Parameter系数预测值
EstimateP值
P value地位级
Site class系数
Parameter系数预测值
EstimateP值
P value6 a 5.880 <0.001 14 a 14.751 <0.001 b 155.907 0.123 b 5.386 <0.001 c 0.265 0.0001 c 0.140 <0.001 8 a 8.109 <0.001 16 a 16.957 <0.001 b 26.642 <0.001 b 4.305 <0.001 c 0.197 <0.001 c 0.133 <0.001 10 a 10.330 <0.001 18 a 19.162 <0.001 b 11.760 <0.001 b 3.630 <0.001 c 0.167 <0.001 c 0.128 <0.001 12 a 12.543 <0.001 20 a 21.366 <0.001 b 7.351 <0.001 b 3.171 <0.001 c 0.151 <0.001 c 0.124 <0.001 表 6 分位数回归模型参数及统计量
Table 6. Parameter estimation and fitting statistics for quantile regression models of site class
地位级
Site class分位数(τ)
Quantile系数
Parameters系数预测值
EstimateP值
P value地位级
Site class分位数(τ)
Quantile系数
Parameters系数预测值
EstimateP值
P valueⅧ 0.01 a 8.192 <0.001 Ⅳ 0.70 a 15.624 <0.001 b 105.787 0.782 b 4.480 <0.001 c 0.220 0.186 c 0.149 <0.001 Ⅶ 0.05 a 11.670 <0.001 Ⅲ 0.85 a 17.412 <0.001 b 10.553 0.046 b 5.112 <0.001 c 0.140 <0.001 c 0.145 <0.001 Ⅵ 0.15 a 13.698 <0.001 Ⅱ 0.95 a 18.427 <0.001 b 4.315 <0.001 b 6.256 <0.001 c 0.102 <0.001 c 0.171 <0.001 Ⅴ 0.30 a 14.457 <0.001 Ⅰ 0.99 a 22.284 <0.001 b 4.350 <0.001 b 4.384 0.008 c 0.119 <0.001 c 0.119 <0.001 表 7 传统方法(左)和分位数回归模型(右)对样地地位级分级的结果
Table 7. The result of site classes grouped by traditional method (left) and quantile regression model (right)
地位级
Site class龄级 Age class 地位级
Site class龄级 Age class 2 3 4 5 6 7 8 9 10 11 2 3 4 5 6 7 8 9 10 11 6 1 0 1 3 0 0 0 0 0 0 Ⅷ 1 0 1 3 0 2 1 0 0 1 8 2 0 1 5 1 2 1 1 0 1 Ⅶ 6 0 1 11 11 4 1 1 1 0 10 5 1 0 11 20 11 1 0 1 0 Ⅵ 10 4 0 5 16 12 0 2 0 1 12 16 6 3 16 32 23 4 3 2 2 Ⅴ 30 5 3 20 39 21 4 2 2 1 14 26 3 2 30 57 26 3 2 2 1 Ⅳ 3 1 2 26 43 21 2 1 2 1 16 3 1 1 25 24 13 4 2 0 0 Ⅲ 0 0 1 23 25 7 3 1 0 0 18 0 0 1 5 3 6 0 0 0 0 Ⅱ 3 1 0 4 1 11 2 1 0 0 20 0 1 0 0 0 1 0 0 0 0 Ⅰ 0 1 1 3 2 4 0 0 0 0 -
[1] 孟宪宇. 测树学(第3版)[M]. 北京: 中国林业出版社, 2006: 99-111. [2] Nicholas N S, Zedaker S M. Expected stand behavior: site quality estimation for southern Appalachian red spruce[J]. Forest Ecology and Management, 1992, 47(1-4): 39-50. doi: 10.1016/0378-1127(92)90264-A [3] 雷相东, 符利勇, 李海奎, 等. 基于林分潜在生长量的立地质量评价方法与应用[J]. 林业科学, 2018, 54(12):119-129. [4] 马 炜, 孙玉军. 长白落叶松人工林立地指数表和胸径地位级表的编制[J]. 东北林业大学学报, 2013, 41(12):21-25. doi: 10.3969/j.issn.1000-5382.2013.12.006 [5] 刘 丹. 基于分布适宜性和潜在生产力的定量适地适树研究[D]. 北京: 中国林业科学研究院, 2018, 15-22. [6] Vanclay J K, Henry N. Assessing site productivity of indigenous cypress pine forest in Southern Queensland[J]. The Commonwealth Forestry Review, 1988, 67(210): 53-64. [7] 周春国, 徐雁南. 地位级表编制的新方法[J]. 华东森林经理, 1997, 11(2):11-13. [8] 黄国胜, 马 炜, 王雪军, 等. 基于一类清查数据的福建省立地质量评价技术[J]. 北京林业大学学报, 2014, 36(3):1-8. [9] Calama R, Canadas N, Montero G. Inter-regional variability in site index models for even-aged stands of stone pine (Pinus pinea L.) in Spain[J]. Annals of Forest Science, 2003, 60(3): 259-269. doi: 10.1051/forest:2003017 [10] 朱光玉, 康 立, 何海梅, 等. 基于树高 - 年龄分级的杉木人工林多形立地指数曲线模型研究[J]. 中南林业科技大学学报, 2017, 37(7):18-29. [11] Koenker R, Bassett G. Regression quantiles[J]. Econometrica, 1978, 46(1): 33-50. doi: 10.2307/1913643 [12] Furno M, Vistocco D. Quantile Regression: Estimation and Simulation[M]. John Wiley & Sons, 2018.3-11. [13] Kocherginsky M, He X, Mu Y. Practical confidence intervals for regression quantiles[J]. Journal of Computational and Graphical Statistics, 2005, 14(1): 41-55. doi: 10.1198/106186005X27563 [14] Mäkinen A, Kangas A, Kalliovirta J, et al. Comparison of treewise and standwise forest simulators by means of quantile regression[J]. Forest Ecology and Management, 2008, 255(7): 2709-2717. doi: 10.1016/j.foreco.2008.01.048 [15] Ducey M J, Knapp R A. A stand density index for complex mixed species forests in the northeastern United States[J]. Forest Ecology and Management, 2010, 260(9): 1613-1622. doi: 10.1016/j.foreco.2010.08.014 [16] Mehtätalo L, Gregoire T G, Burkhart H E. Comparing strategies for modeling tree diameter percentiles from remeasured plots[J]. Environmetrics, 2008, 19(5): 529-548. doi: 10.1002/env.896 [17] Bohora S B, Cao Q V. Prediction of tree diameter growth using quantile regression and mixed-effects models[J]. Forest Ecology and Management, 2014, 319: 62-66. doi: 10.1016/j.foreco.2014.02.006 [18] Cao Q V, Wang J. Calibrating fixed- and mixed-effects taper equations[J]. Forest Ecology and Management, 2011, 262(4): 671-673. doi: 10.1016/j.foreco.2011.04.039 [19] Lim K S, Treitz P M. Estimation of above ground forest biomass from airborne discrete return laser scanner data using canopy-based quantile estimators[J]. Scandinavian Journal of Forest Research, 2006, 19(6): 558-570. [20] Zang H, Lei X, Zeng W. Height–diameter equations for larch plantations in northern and northeastern China: a comparison of the mixed-effects, quantile regression and generalized additive models[J]. Forestry, 2016, 89(4): 434-445. doi: 10.1093/forestry/cpw022 [21] Özçelik R, Cao Q V, Trincado G, et al. Predicting tree height from tree diameter and dominant height using mixed-effects and quantile regression models for two species in Turkey[J]. Forest Ecology and Management, 2018, 419(419-420): 240-248. [22] Fang Z, Bailey R L. Height–diameter models for tropical forests on Hainan Island in southern China[J]. Forest Ecology and Management, 1998, 110(1-3): 315-327. doi: 10.1016/S0378-1127(98)00297-7 [23] Huang S, Price D, J. Titus S. Development of ecoregion-based height–diameter models for white spruce in boreal forests[J]. Forest Ecology and Management, 2000, 129(1-3): 125-141. doi: 10.1016/S0378-1127(99)00151-6 [24] Newton P F, Amponsah I G. Comparative evaluation of five height–diameter models developed for black spruce and jack pine stand-types in terms of goodness-of-fit, lack-of-fit and predictive ability[J]. Forest Ecology and Management, 2007, 247(1-3): 149-166. doi: 10.1016/j.foreco.2007.04.029 [25] Lei X, Peng C, Wang H, et al. Individual height–diameter models for young black spruce (Picea mariana) and jack pine (Pinus banksiana) plantations in New Brunswick, Canada[J]. The Forestry Chronicle, 2009, 85(1): 43-56. doi: 10.5558/tfc85043-1 [26] 孙玉军, 王新杰, 马 炜. 林改区域典型树种森林碳储量监测技术研究[M]. 北京: 中国林业出版社, 2014: 15-29. [27] Roger Koenker, Machado J A F. Goodness of fit and related inference processes for quantile regression[J]. Journal of the American Statistical Association, 1999, 94(448): 1296-1310. doi: 10.1080/01621459.1999.10473882 [28] Zhang B, Sajjad S, Chen K, et al. Predicting tree height-diameter relationship from relative competition levels using quantile regression models for Chinese fir (Cunninghamia lanceolata) in Fujian Province, China[J]. Forests, 2020, 11(2): 183. doi: 10.3390/f11020183 -



 下载:
下载:














